STA 6166 UNIT 3 Section 3 Answers

Welcome

<

Begin

<

Section 3

<

Unit 3 Section 3 Answers

To Ag and Env. Answers

To Tox and Health Answers

To Social and Education Answers

To Engineering Answers

 

Unit 3 Section 3 Answers

Tox and Health

1. In a study of children aged 0 to15, concern is focused on the presence or absence of the carrier for Streptococcus Pyogenesis and the relationship between the presence of the carrier and tonsil size.  

	Tonsils present. Not enlarged	Tonsils enlarged
Presence of the carrier	15	19
Absence of the carrier	380	360
Total number	395	379

a. Is the presence of the carrier related to whether tonsils are enlarged or not. Test this hypothesis at the P(Type I error)=a=.05 level.

H₀: p_Not - p_Enlarged = 0

H_A: p_Not - p_Enlarged not equal to 0

T.S.:

RR: Reject if |z| > z_a/2=z_0.025 = 1.96

Here, the test statistic value is 0.823 which is less than 1.96 causing us to NOT reject the null hypothesis and conclude that there is no difference in carrier rates for children with enlarged tonsils versus children without enlarged tonsils. This suggests that children with enlarged tonsils have no higher incidence of the carrier of Streptococcus Pyogenesis than do children without enlarged tonsils.

b. Calculate a 95% confidence interval for the difference between the Tonsils enlarged probabilities in the presence of the carrier versus that in the absence of the carrier.

 

The 95% confidence interval is computed using the equation:

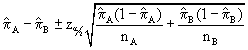
[0.2988 ± 1.96(0.09329)] or [0.2988 ± 0.1828] or [0.1159, 0.48165]

Note that the 95% CI does not contain zero, a good indication that the difference is not statistically equal to zero.

 2. In a controlled clinical trial to determine the efficiency of an experimental drug for treating migraine headache, patients were divided into four groups and were treated with four drugs: A, B, C and D. Each treatment lasted 12 weeks. At the end of the treatment period, the effect of the drug was classified into two categories:  effective and not effective. The migraine headache data obtained are as follows: 

 

Drug	Effective	Total
A	26	45
B	14	28
C	10	17
D	22	90

Use these data to run a chi-square test to determine whether the effectiveness of all drugs are the same.This is equivalent to testing that all effectiveness proportions are the same.

These data represent a a 2 by 4 contingency table only not in traditional format. We could write the table as follows instead.

		Effective
		Yes	No
Drug	A	26	19
	B	14	14
	C	10	7
	D	22	68

We will perform the Chi Square analysis using Excel to make the calculations. A copy of the spreadsheet follows. Note that we first compute the row and column proportions which are not particularly important to computing the Chi Square statistic but will be useful in interpreting it. Next we compute the expected values, then the Chi Square values and in that table we sum all the cells in the table to get the overall Chi Square statistic.

Frequency		Effective
	Drug	Yes	No	Total
	A	26	19	45
	B	14	14	28
	C	10	7	17
	D	22	68	90
	Total	72	108	180
Column Proportions		Effective
	Drug	Yes	No
	A	0.3611	0.1759
	B	0.1944	0.1296
	C	0.1389	0.0648
	D	0.3056	0.6296
	Total	1	1
Row Proportions		Effective
	Drug	Yes	No	Total
	A	0.5778	0.4222	1
	B	0.5000	0.5000	1
	C	0.5882	0.4118	1
	D	0.2444	0.7556	1
	Total
Expectations		Effective
	Drug	Yes	No	Total
	A	18.0	27.0	45
	B	11.2	16.8	28
	C	6.8	10.2	17
	D	36.0	54.0	90
	Total	72	108	180
Differences		Effective
	Drug	Yes	No	Total
	A	8	-8	0
	B	2.8	-2.8	0
	C	3.2	-3.2	0
	D	-14	14	0
	Total	0	0	0
Chi Square Values		Effective
	Drug	Yes	No	Total
	A	3.5556	2.3704
	B	0.7000	0.4667
	C	1.5059	1.0039
	D	5.4444	3.6296
	Total			18.67647
				Overall Chi Square Value
DF = (r-1)(c-1) =	3
Type I error rate=	0.05
Chi Square Critical value=		7.815

We find from above that the Chi Square test statistic value is 18.676 and the critical value for the rejection region is 7.815. Hence we reject the null hypothesis and conclude that there effectiveness is not independent of drug. This suggests that different drugs have different effectiveness. The Chi Square values in each cell tell us which drug by effectiveness combinations we should be looking at. The larger the value, the more the observed count differs from the expected count. Clearly we should be looking at drug D and drug A. Drug D is clearly less effective than expected, whereas Drug A is slightly more effective than expected. From the row percentages we see that Drugs A, B and C are 50% or more effective, whereas Drug D is only half that effective at 24%. The most effective drug was C, but it is also the one for which we have the least information.