|
STA
6166 UNIT 3 Section 3 Answers
|
| Welcome | < | Begin | < | < | Unit 3 Section 3 Answers | |||||
| To Ag and Env. Answers |
| To Tox and Health Answers |
| To Social and Education Answers |
| To Engineering Answers |
Unit 3 Section 3 Answers
Engineering
1. A project manager for an engineering firm submits a bid for engineering
design for two projects. The firm formally evaluates the chances that each
bid will be accepted by surveying its engineers. The following table summarizes
the collective assessment from this survey.
| Results of bids |
Project A
|
Project B
|
| Accepted |
28
|
25
|
| Refused |
29
|
24
|
| Total number of bits submitted |
57
|
49
|
a. Test whether the chances that each bid was accepted are different. Use a=.05.
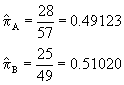
H0: pA - pB = 0
HA: pA - pB not equal to 0
T.S.: 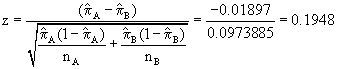
RR: Reject if |z| > za/2=z0.025 = 1.96
Conclusion: Do NOT reject the null hypothesis and conclude that the proportion saying the bids will be accepted is the same for the two projects. Note that from this we would also conclude that the proportion suggesting the bids will not be accepted for the two projects should also be considered the same.
b. Calculate a 95% confidence interval for the difference of chances that each bid was accepted.
The 95% confidence interval is computed using the equation:
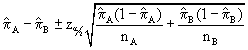 or [-0.01897±1.96(0.09739)] or [-0.2098, 0.1719]
or [-0.01897±1.96(0.09739)] or [-0.2098, 0.1719]
2. A study plans to assess the impact of several factors
involving the heat treatment of leaf springs. In this process, a conveyor
system transports leaf spring assemblies through a high-temperature furnace.
After heating, a high-pressure press induces curvature in the medal. Once
the spring leaves the press, an oil quench cools it to near ambient temperature.
An important quality characteristic of this process is the resulting free
height of the spring. The researchers are interested in examining four factors
known to affect this free height. For each spring tested, the final classification
is whether the spring is below the specified minimal spring height. Results
of numerous tests are given in the following table.
|
Factors |
Low level |
Total |
|
1.High heat temp. |
14 |
32 |
|
2.heating
time |
23 |
48 |
|
3.Transfer
time |
10 |
22 |
|
4.Hold
down time |
2 |
5 |
Use these data to run a Chi-square test to determine whether a finding of low level is independent of the factors used. Use a=.05.
These data represent a 2 by 4 contingency table but is presented in odd format. More commonly you would expect to see a table like the one below.
|
Spring Height
|
|||
| Low | Acceptable | ||
| Factor |
High Heat Temp
|
14 | 18 |
|
Heating Time
|
23 | 25 | |
|
Transfer Time
|
10 | 12 | |
|
Hold Down Time
|
2 | 3 | |
We will use SAS to analyze these data. The SAS program follows. Note that each factor by spring height combination forms an observation in the data set and the response is the number found to be in that combination. The TABLE statement in PROC FREQ procedure computes the 2 x 4 table, the WEIGHT statement tells us that for each factor x height combination there are NUMBER responses and the "/CHISQ" option on the TABLE statement request the forma Chi Square test.
data spring; input factor $ height $ number ; datalines; hht l 14 hht a 18 ht l 23 ht a 25 tt l 10 tt a 12 hdt l 2 hdt a 3 ; datalines; proc freq data=spring; table factor*height / chisq; weight number; run;
The output from this program is as follows:
The FREQ Procedure
Table of factor by height
factor height
Frequency|
Expected |
Percent |
Row Pct |
Col Pct |a |l | Total
---------|--------|--------|
hdt | 3 | 2 | 5 <- observed frequencies
| 2.7103 | 2.2897 | <- expected frequencies
| 2.80 | 1.87 | 4.67
| 60.00 | 40.00 |
| 5.17 | 4.08 |
---------|--------|--------|
hht | 18 | 14 | 32
| 17.346 | 14.654 |
| 16.82 | 13.08 | 29.91
| 56.25 | 43.75 |
| 31.03 | 28.57 |
---------|--------|--------|
ht | 25 | 23 | 48
| 26.019 | 21.981 |
| 23.36 | 21.50 | 44.86
| 52.08 | 47.92 |
| 43.10 | 46.94 |
---------|--------|--------|
tt | 12 | 10 | 22
| 11.925 | 10.075 |
| 11.21 | 9.35 | 20.56
| 54.55 | 45.45 |
| 20.69 | 20.41 |
---------|--------|--------|
Total 58 49 107
54.21 45.79 100.00
Statistics for Table of factor by height
Statistic DF Value Prob
------------------------------------------------------
Chi-Square 3 0.2096 0.9760 <- This is the Chi Square test statistic
Likelihood Ratio Chi-Square 3 0.2102 0.9759 and p-value
Mantel-Haenszel Chi-Square 1 0.0763 0.7824
Phi Coefficient 0.0443
Contingency Coefficient 0.0442
Cramer's V 0.0443
WARNING: 25% of the cells have expected counts less
than 5. Chi-Square may not be a valid test.
Sample Size = 107
The Chi Square value of 0.2096 has an associated p-value of 0.976 which is much greater than the 0.05 level chosen for the Type I error rate. This suggests that we do NOT reject the null hypothesis of independence. This is further supported when we consider the very small differences between the observed and expected frequencies in the table. Note that the results of the Chi Square analysis is thrown into doubt since a number of the cells have expected counts less than 5. We could consider redoing the analysis without this category to see if it makes a difference in the results. When we do this we calculate a Chi Square statistic value of 0.1386 with associated p-value of 0.933. Our conclusions do not change.
Concluding that the level of factor is independent of the height of spring suggests that none of these factors can be used to control the height of the spring. We must continue to look for other factors.