Experiment Result	Method A	Method B
Good	134	207
Defective	16	33
Total number	150	240

a. Use these data to test whether the proportion of GOOD onions in each method are different from each other. Use a=.05.

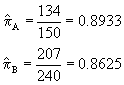
H₀: p_A - p_B = 0

H_A: p_A - p_B not equal to 0

T.S.: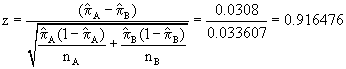

RR: Reject if |z| > z_a/2=z_0.025 = 1.96

Conclusion: Do NOT reject the null hypothesis and conclude that the proportion of good onions is the same for the two methods. Note that from this we would also conclude that the proportion of bad onions should also be considered the same.

b. Calculate a 95% confidence interval for the difference tested above.

The 95% confidence interval is computed using the equation:

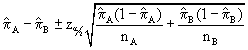
2. A second aspect of the study was to examine the effects of different fertilizer treatments on the incidence of blackleg (Bacterium phytotherum) on potato seedlings. Seedlings were randomly assigned to a fertilizer treatment and after three weeks classified as to whether it was contaminated by blackleg or free. The results for four treatment were as follows:

Observed frequencies	Blackleg	Total
1.No fertilizer	16	101
2.Nitrogen only	10	95
3.Dung only	4	113
4.Nitrogen and dung	14	141

Use these data to determine if the presence of Blackleg is independent of the Fertilization method. Use a=.05.

These data represent a 2 by 4 contingency table but is presented in odd format. More commonly you would expect to see a table like the one below.

		Disease Status
		Blackleg	Clean
Fertilization	No Fertilizer	16	85
	Nitrogen Only	10	85
	Dung Only	4	109
	Nitrogen&Dung	14	127

Using Minitab we first enter the data in table form.

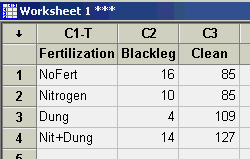
Next, using the command STAT > TABLES > CHI SQUARE TEST, we select C2 and C3 and proceed to perform the Chi Square test for association.

Chi-Square Test: Blackleg, Clean

Expected counts are printed below observed counts

      Blackleg    Clean    Total
    1       16       85      101
          9.88    91.12                  <- Expected counts = n(i,.)*n(.,j)/n(.,.)
    2       10       85       95            n(i,.) is row i total (101,95,113 or 141)
          9.29    85.71                     n(.,j) is column j total (44 or 406)
    3        4      109      113            n(.,.) is overall total = 450
         11.05   101.95
    4       14      127      141
         13.79   127.21
Total       44      406      450

Chi-Sq =  3.798 +  0.412 +
          0.054 +  0.006 +
          4.497 +  0.487 +
          0.003 +  0.000 = 9.258   <- Chi Square test statistic (see Page 504).
DF = 3, P-Value = 0.026            <- p-value is less than Type I error rate suggesting we 
                                      reject the null hypothesis of independence and conclude
                                      that the Presence of Blackleg is not independent of 
                                      fertilization.
                        

Note that once we reject the null hypothesis of independence we start to look for where the dependency exists. If we compare the expected frequencies to the observed frequencies we find that we had more Blackleg with the NO fertilization treatment (obs: 16, exp: 10) than expected and less Blackleg with the Dung only fertilization than expected (obs:4, exp: 11). This suggests that any fertilizer will provide some protection for Blackleg but Dung might actually reduce the occurrance.