ANSWERS
Computations for this problem set will be done in SAS.
The SAS program can be found here. The output found here.
1. a. Use these data to test the research hypothesis that there is a difference in mean hay consumption for the two diets. Use a = 0.05.
Statistics
Lower CL Upper CL Lower CL Upper CL
Variable treatment N Mean Mean Mean Std Dev Std Dev Std Dev Std Err Minimum Maximum
response Group_1 8 13.616 14.538 15.459 0.7285 1.1019 2.2426 0.3896 12.8 15.9
response Group_2 8 7.6276 8.375 9.1224 0.5911 0.894 1.8196 0.3161 6.8 9.5
response Diff (1-2) 5.0865 6.1625 7.2385 0.7346 1.0033 1.5824 0.5017
T-Tests
Variable Method Variances DF t Value Pr > |t|
response Pooled Equal 14 12.28 <.0001
response Satterthwaite Unequal 13.4 12.28 <.0001
The p-value reported here is for the two-sided hypothesis. With this very small p-value, we would conclude that the hypothesis that the two groups have similar hay consumption levels should be rejected. Even a one-sided hypothesis that Group_1 mean is greater than the Group_2 mean would result in rejection. The critical value from a t-table would be t(0.05,14)=1.761 and t(0.05,13)=1.771 respectively. The observed critical value of 12.28 is way into the rejection region. Note that the standard deviations for the two groups are not very different.
1. b. Provide an estimate of the amount of difference in the mean hay consumption of the two groups.
Our best estimate is the difference between the sample means of the two groups. In this case, 6.1625. An interval estimate can be given as the 95% confidence interval for the difference which is computed as (5.0865, 7.2385). Note that zero is not a part of this interval, another indication that the Group_1 consumption is significantly greater than the Group_2 consumption.
2. Using the data from problem 6.75, perform the Wilcoxon rank sum test. Do the t-test and Wilcoxon test give different results?
The output from SAS is duplicated below:
Wilcoxon Scores (Rank Sums) for Variable response
Classified by Variable treatment
Sum of Expected Std Dev Mean
treatment N Scores Under H0 Under H0 Score
---------------------------------------------------------------------------
Group_1 8 100.0 68.0 9.521905 12.50
Group_2 8 36.0 68.0 9.521905 4.50
Wilcoxon Two-Sample Test
Statistic 100.0000
Normal Approximation
Z 3.3082
One-Sided Pr > Z 0.0005
Two-Sided Pr > |Z| 0.0009
t Approximation
One-Sided Pr > Z 0.0024
Two-Sided Pr > |Z| 0.0048
Z includes a continuity correction of 0.5.
We can test both the two-sided alternative hypothesis or the one-side hypothesis that Group_1 median consumption is greater than that of Group_2. The test statistic for both tests is the set of ranks for Group_1, in this case T=100. With samples of size 8 we can use the Table 5 in the book to look up the critical values (TL=48,Tu=87) for the a=0.05 two sided test and (TL=52, Tu=84) for the one-sided a=0.05 test. In both cases, T=100 is greater than Tu suggesting that we would reject the null hypothesis of no differences in group medians. In this case, both the Wilcoxon and t-tests lead to the same conclusions.
3. What is the 95% confidence interval for the difference between the two means?
An interval estimate can be given as the 95% confidence interval for the difference which is computed as (5.0865, 7.2385). Note that zero is not a part of this interval, another indication that the Group_1 consumption is significantly greater than the Group_2 consumption.
4. How many dairy cows would be needed for each group if we wanted to know the average difference between the two groups to within plus or minus .5 kg with 95% confidence (Hint see page 314). Use the pooled variance estimate from the t-test as if it were the true variance.
We will assume the common variance for the two groups is the pooled variance. Note that the SAS output does not provide us with this number so we will have to compute it from its equation given on page 268 in the book.

Using the equation from page 314 we have
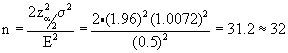
suggesting that we would need 32 cattle in EACH group to reach this level of precision in the average difference between the two groups.