Mathematical Finance Program
Research in Mathematical Finance
Research in the Texas Tech Mathematical Finance program is focused on both risk management (‘beta’ in Wall Street terminology) and ‘alpha generation’ (the Street term for trading strategies for making money). Current research projects by members of the MF group fall in the following areas.
1. Reconciling behavioral finance, market microstructure, and dynamic asset pricing
(Abootaleb Shirvani, Y. Hu, W. Brent Lindquist, Frank J. Fabozzi and Svetlozar T. Rachev)
This project has an overarching goal of unifying the seemingly contradictory theoretical bases for the major fields of rational and behavioral finance. For example, current dynamic models for asset pricing are ‘amazingly free’ of any variables that describe the very short-term behavior (microstructure) of markets. This arises in part because existing continuum asset pricing models assume trades can occur continuously with no transaction costs or other barriers.
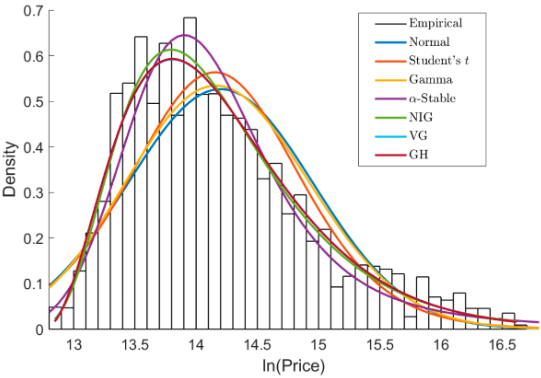
1A. Multiple Subordinated Modeling of Asset Returns
According to behavioral finance theory, investor views should be taken into account in models of the underlying asset processes. For example, investors view positive and negative returns differently according to disposition effects (such as the manner in which investors treat capital gains). Thus, to obtain more realistic asset prices, it is essential to incorporate investor views in log-return and option pricing models. To be consistent with dynamic asset pricing theory, investor views can be accounted for by introducing an intrinsic time process, which we refer to as a behavioral subordinator. The process is subordinated to the Brownian motion process in the well-known log-normal model, resulting in a new log-price process. In addition to incorporating investor views, the additional subordinator enables the capture of rare events of the stock return distribution that cannot be explained well by the existing one-layer subordinated model.

1B. Resolution of Financial Puzzles within Rational Finance
Proponents of behavioral finance have pointed to historical behaviors of the stock market that are inconsistent with rational finance theory as evidence for the failure of rational finance. These empirical observations are referred to as “puzzles”. The three most striking puzzles are the equity premium puzzle, the stock price predictability puzzle, and the volatility puzzle. In this project, we offer a resolution to these puzzles within the context of rational finance. We empirically show that the market’s inefficiency, attributable to the equity premium puzzle and volatility of excess return across time, is caused by fitting an improper distribution to the historical returns. We offer a statistical model within the context of rational finance that can be used without relying on behavioral finance assumptions to model stock returns predictability.
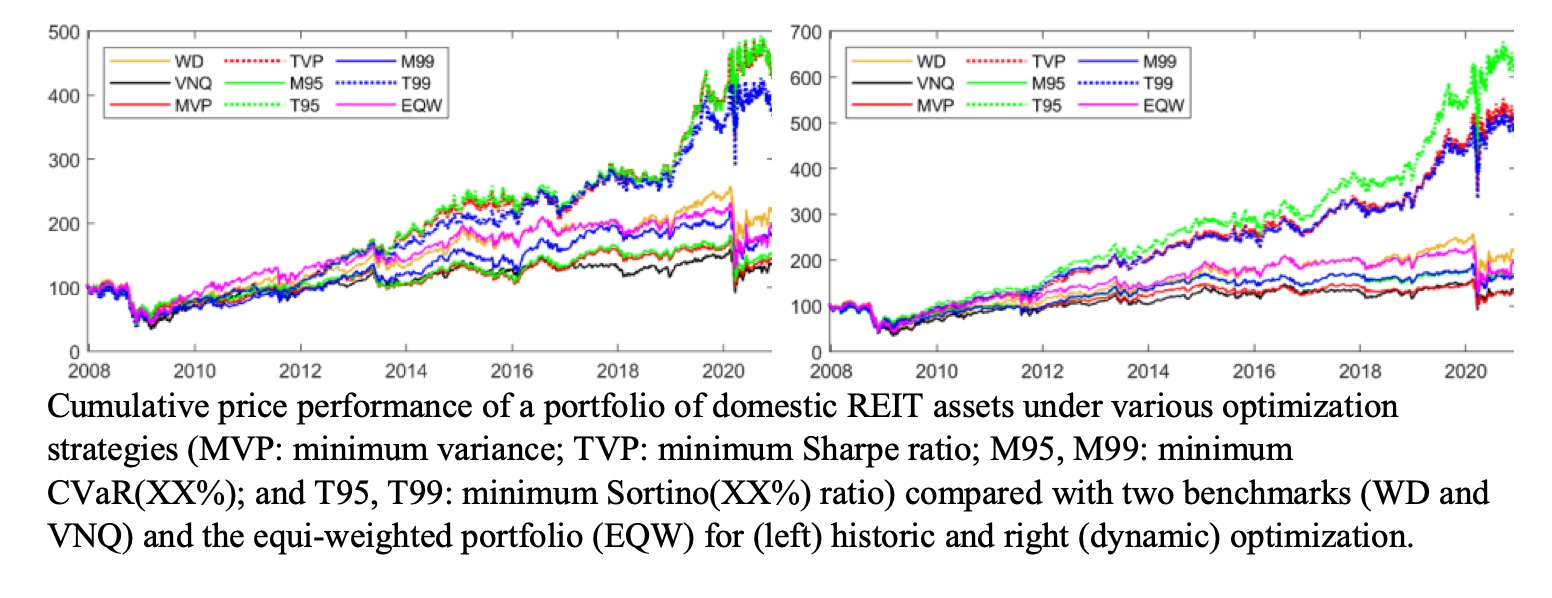
2. Risk analytics and optimal portfolios for REITs
(Abootaleb Shirvani, Yuan Hu, W. Brent Lindquist and Svetlozar T. Rachev)
This project looks at the application of modern portfolio theory and risk analytics to portfolios composed of shares of real estate investment trusts. It is the first stage of a global project on risk analytics and optimal portfolio construction in the real estate market. It will be followed by (ii) modeling and forecasting real estate prices with hedonic statistical and econometric methods and (iii) asset liability management for the real estate market.
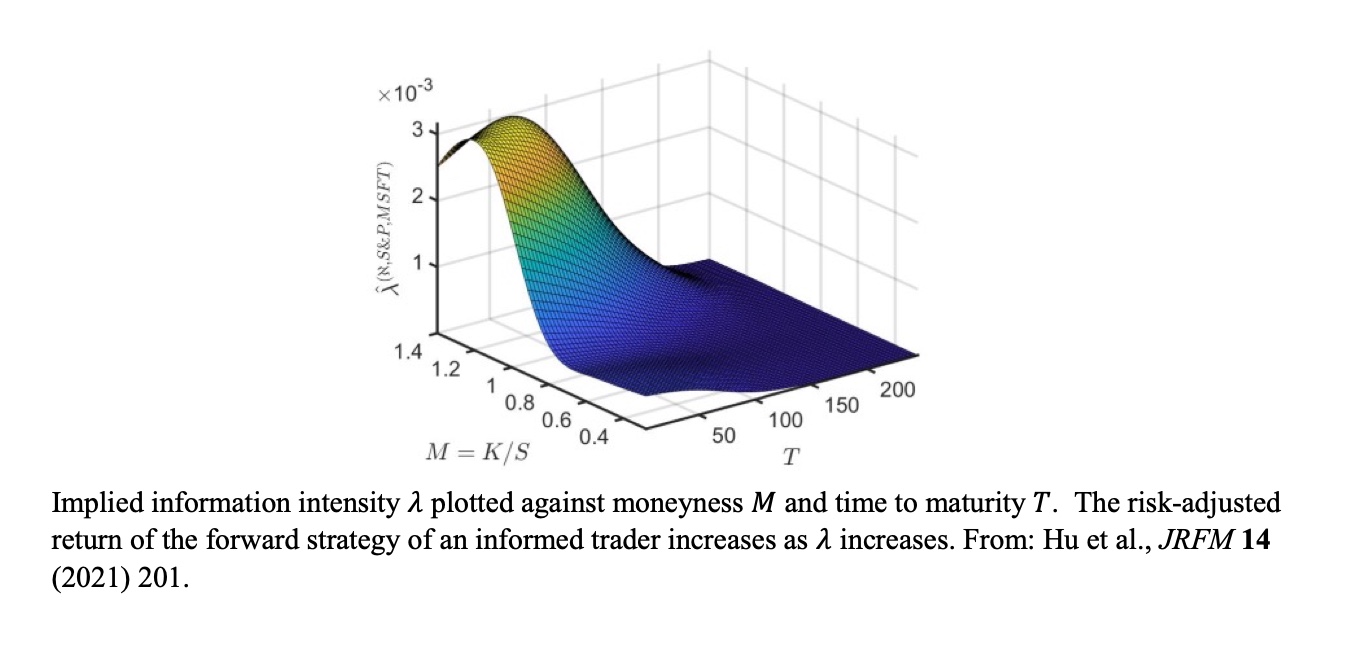
3. Option pricing in an investment setting
(Abootaleb Shirvani, Y. Hu, W. Brent Lindquist, Frank J. Fabozzi, and Svetlozar T. Rachev)
The classical European-style option pricing approach assumes that the sole goal of the hedger (who takes the short position in an option contact) is to perfectly replicate perfectly (in a complete market setting) the short position’s liability. The goal of this project is to dynamically optimize the hedger portfolio so that the liability at the option expiration time is perfectly hedged while collecting risk-adjusted return until the termination of the option contract.
4. A new class of statistical measures for distributional tail dependence
(Davide Lauria, Alex Trindale, and Svetlozar T. Rachev)
The classical measures for distributional tail dependence, such as the coefficients for lower and upper tail dependence, lose their significance if the distributional tails are thinner than that specified by power-law decay (so-called regularly varying tails). This work is focused on introducing and testing a new class of tail measures which are well defined and meaningful for pairs of random variables having an arbitrary distributional tail. The work will be extended to dynamic tail measures and in dimension larger than two.
5. Developing non-traditional market indices
A market index is a carefully chosen portfolio of investment holdings that represents (a segment of) a financial market. The calculation of the index value derives from a valuation of the underlying holdings. (In traditional financial markets, these would be the prices of shares held in the index portfolio.) Investors cannot invest directly in an index, as the index value is used solely as a benchmark to gauge the movements of a market or market segment and for developing tradable, index-based funds in which investing can occur. Once index-based funds exist, then derivatives, such as call and put options, can be developed and priced using the index-based fund as the underlying asset. This allows investors to implement insurance strategies against adverse market conditions. This project has the overarching goal for developing indices for non-traditional “markets” that have huge financial impacts. Generally, index valuation is based on a simple method (such as equal or market capital weighting of the values of the assets in the portfolio). We seek to employ risk-minimizing or return-maximizing valuation methods based upon modern portfolio theory.
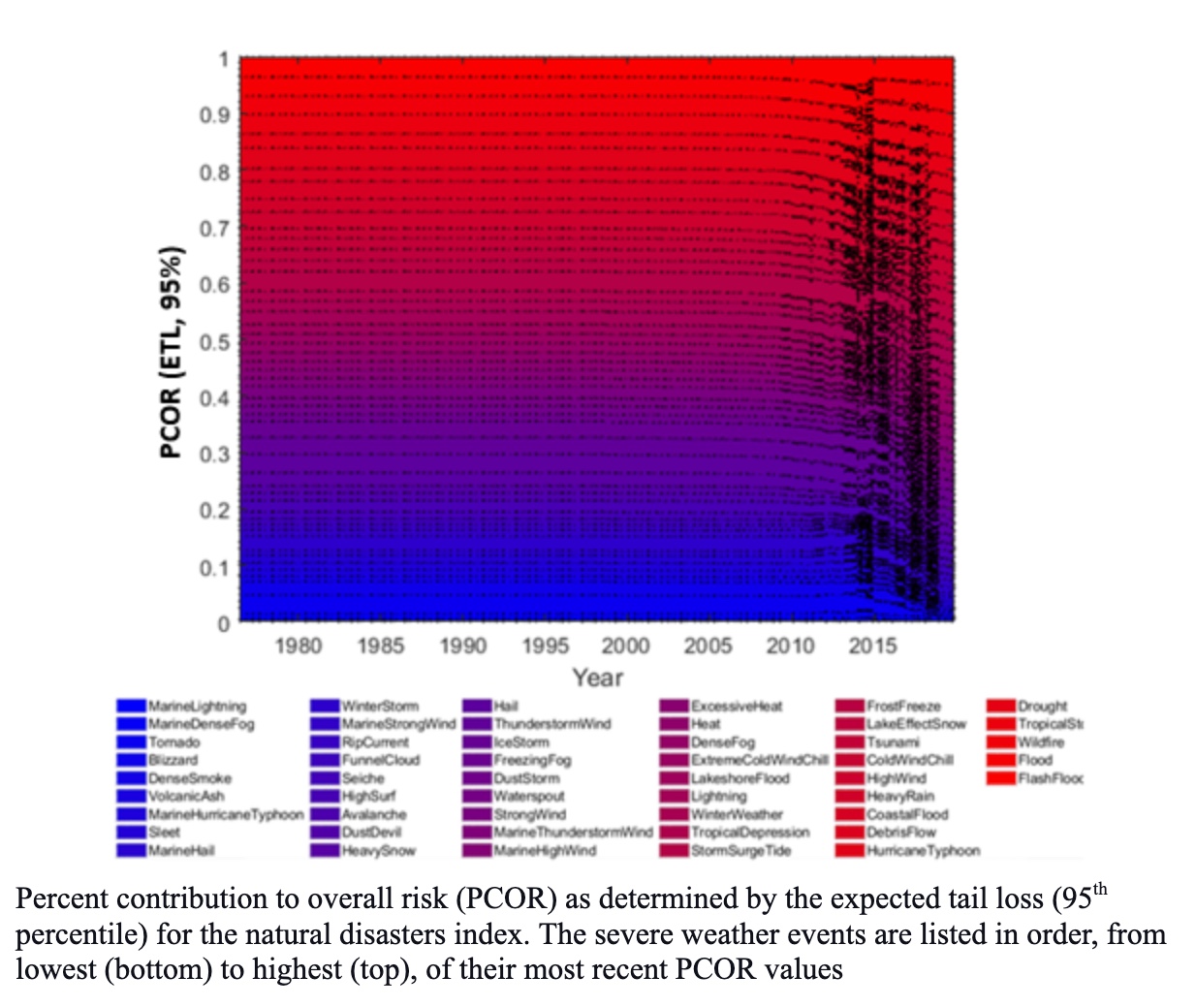
5A. Indices on financial losses caused by natural disasters and crime
(Thilini Mahanama, Abootaleb Shirvani, and Svetlozar T. Rachev)
This project is aimed at the development of index-based insurance portfolios for natural disasters and crime in the United States by taking their economic impacts into account. Underlying the indices, investments would be hedged by issuing marketable options and providing risk budgets. The performance of each index is evaluated to determine its resilience to economic crises. The indices are intended to help investors gauge investment risk based on their desired risk level and provide hedge strategies for potential losses due to economic crashes.
5B. An ESG Index
(Thilini Mahanama, Abootaleb Shirvani, Yuan Hu , W. Brent Lindquist, and Svetlozar T. Rachev)
There is a strong societal push for investing in market segments that reflect social responsibility, such as environmental sustainability and human rights. Strongly related to this are corporate governance attitudes. Socially responsible investing relies on portfolios comprised solely of assets that reflect such investor attitudes. We consider the development of an environmental, social, and corporate governance (ESG) market index based on CVaR(99%) portfolio optimization and normal compound NIG dynamics.
5C. Market Volatility Index
(Abootaleb Shirvani, Y. Hu, W. Brent Lindquist, Frank J. Fabozzi, and Svetlozar T. Rachev)
The goal of this project is to create an Index to measure the actual market volatility. The VIX index is a popular measure of the stock market’s expectation of volatility based on S&P 500 index options. It is calculated and disseminated on a real-time basis by the Chicago Board Options Exchange, and is often referred to as the fear index or fear gauge. The VIX index measures the implied volatility of the S&P 500 Index and does not measure actual market volatility. VIX has been criticized as a reliable predictor of future volatility; it has been described instead as a measure of the current price of index options. Our research is focused on creating an index to measure actual market volatility. We investigate construction of this index from three options: (i) exchange traded funds, (ii) the actual volatility of the 500 large companies comprising the S&P 500, and (iii) the actual volatility of the 30 companies comprising the Dow Jones Industrial Average, in order to detect the best representative of actual market volatility and perhaps a fundamental index for the markets.
6. Hedonic Modeling of Real Estate Prices
(Jason R. Bailey, W. Brent Lindquist, and Svetlozar T. Rachev)
The goal of this project is to analyze real estate prices based on traditional (e.g., number of bedrooms, number of bathrooms) and non-traditional (e.g., environmental, governance) input factors. We use various hedonic models to do so. We contrast the commonly used Generalized Linear Model (GLM) against a more sophisticated Generalized Additive Model (GAM). The GAMs consistently outperform the GLMs, which is notable given that many input factors may not be linear. City-dependent results, especially for Environmental, Social, and Governance (ESG) factors are present for many of the analyzed cities. In evaluating relevant input factors and predictive models, we can improve the price-estimating tools currently in use in the real estate space.
Recent Publications by the Texas Tech Mathematical Finance group
J. R. Bailey, W. B. Lindquist and S. T. Rachev. Hedonic models incorporating ESG factors for time series of average annual home prices. J. Risk Financial Manag. 17 (2024) 375. https://doi.org/10.3390/jrfm17080375
D. Lauria, J. Park, Y. Hu, W. B. Lindquist, S.T. Rachev, and F.J. Fabozzi. An empirical implementation of the shadow riskless rate. Risks. 12 (2024) 187. https://doi.org/10.3390/risks12120187
W. B. Lindquist and S. T. Rachev. Alternatives to classical option pricing. Ann. Oper. Res. (2024) https://doi.org/10.1007/s10479-024-06213-z
W. B. Lindquist, S. T. Rachev, J. Gnawali, and F. J. Fabozzi. Dynamic asset pricing in a unified Bachelier-Black-Scholes-Merton model. Risks 12 (2024) 136. https://doi.org/10.3390/risks12090136
A. Shirvani, S. Mittnik, W.B. Lindquist, and S.T. Rachev. Bitcoin volatility and intrinsic time using double-subordinated Lévy processes. Risks 12 (2024) 82. https://doi.org/10.3390/risks12050082
Y. Hu, W. B. Lindquist, S. T. Rachev, and F. J. Fabozzi. Option pricing using a skew random walk pricing tree. J. Risk Financial Manag. 17 (2024) 138. https://doi.org/10.3390/jrfm17040138
Y. Hu, W.B. Lindquist and S.T. Rachev. Sustainability-valued discrete option pricing in complete markets. J. Sustain. Finance Invest. (2024) 1-35. https://doi.org/10.1080/20430795.2024.2330518
T. V. Mahanama, A. Shirvani, S. Rachev, and F. J. Fabozzi. The financial market of indices of socioeconomic well-being, Journal of Risk and Financial Management 17 (1), 35, https://doi.org/10.3390/jrfm17010035 (2024)
Y. He, Y. Hu, and S. Rachev The implied views of bond traders on the spot equity market, Frontiers in Applied Mathematics and Statistics 9, 1324079, https://doi.org/10.3389/fams.2023.1324079 (2023)
N. A. Nyarko, B. Divelgama, J. Gnawali, B. Omotade, S. T. Rachev, and P. Yegon. Exploring dynamic asset pricing within Bachelier’s market model, Journal of Risk and Financial Management 16 (8), 352. (2023)
L. B. Klebanov, Y. V. Kuvaeva-Gudoshnikova, and S.T. Rachev. Heavy-tailed probability distributions: Some examples of their appearance, Mathematics 11 (14), 3094. (2023)
Y. He and S. Rachev. Exploring implied certainty equivalent rates in financial markets: Empirical analysis and application to the electric vehicle industry, Journal of Risk and Financial Management 16 (7), 344. (2023)
N. Abudurexiti, K. He, D. Hu, S. T. Rachev, H. Sayit, and R. Sun. Portfolio analysis with mean-CVaR and mean-CVaR-skewness criteria based on mean–variance mixture models, Annals of Operations Research, 2023/5/30, 1–22. (2023)
L. Klebanov and S. T. Rachev. Generalized hyperbolic distributions, Journal of Risk and Financial Management 16 (4), 251. (2023)
J.R. Bailey, D. Lauria, W.B. Lindquist, S. Mittnik, S.T. Rachev. Hedonic models of real estate prices: GAM models; environmental and sex-offender-proximity factors. J. Risk Financial Manag., 15 (2022) 601. https://doi.org/10.3390/jrfm15120601
W.B. Lindquist, S.T. Rachev, Y. Hu, and A. Shirvani. Advanced REIT Portfolio Optimization: Innovative Tools for Risk Management. Dynamic Modeling and Econometrics in Economics and Finance, Vol. 30. Cham; Springer (2022). ISBN: 978-3031152856; (258
pages). https://doi.org/10.1007/978-3-031-15286-3
Y. Hu, W.B. Lindquist, S.T. Rachev, A. Shirvani, and F.J. Fabozzi. Market complete option valuation using a Jarrow-Rudd pricing tree with skewness and kurtosis. J. Econ. Dyn. Control. 137 (2022), 104345
T. Mahanama, A. Shirvani, A. and S. Rachev. A Natural Disasters Index. Environmental Economics and Policy Studies, 137, 104345, (2022) https://doi.org/10.1007/s10018-021-00321-x
Belhad, A., Lauria, D. and Trindade, A.A. (2022), “Nonparametric Estimation of Systemic Risk Via Conditional Value-at-Risk”, The Journal of Risk, 25(1), 1–21.
S.V. Stoyanov, S.T. Rachev, A Shirvani, F.J. Fabozzi. Option pricing in an investment risk-return setting. Applied Economics, 1-14. DOI: 10.1080/00036846.2021.1980490. (2022)
A. Shirvani, F.J. Fabozzi, B. Racheva-Iotova, and S.T. Rachev. Option pricing with greed and fear factor: The rational finance approach, Journal of Derivatives 29 (2), 77–119, (2021) https://doi.org/10.3905/jod.2021.1.138.
Y. Hu, W.B. Lindquist and F.J. Fabozzi. Modelling price dynamics, optimal portfolios, and option valuation for crypto assets. J. Altern. Invest., 24 (2021), 75-93. https://doi.org/10.3905/jai.2021.1.133
Y. Liu, P. M. Djurić, Y. S. Kim, S. T. Rachev, and J. Glimm. Systemic risk modeling with Lévy copulas, Journal of Risk and Financial Management 14 (6), 251. (2021)
Y. Hu, W.B. Lindquist and F.J. Fabozzi. Modelling price dynamics, optimal portfolios, and option valuation for crypto assets. J. Altern. Invest., 24 (2021), 75-93. https://doi.org/10.3905/jai.2021.1.133
T. Mahanama, A. Shirvani, and S. Rachev. Global index on financial losses due to crime in the United States, J. Risk Financial Manag. 14 (7), 315, (2021). https://doi.org/10.3390/jrfm14070315
Y. Hu, W.B. Lindquist and S.T. Rachev (2021). Portfolio optimization constrained by performance attribution. J. Risk Financial Manag., 14 (2021) 201. DOI: https://doi.org/10.3390/jrfm14050201.
A. Shirvani, S.V. Stoyanov, F.J. Fabozzi, and S.T. Rachev (2021). Equity premium puzzle or faulty economic modelling? Rev. Quant. Finan. Acc. 56, 1329-1342. DOI: 10.1007/s11156-020-00928.
A. Shirvani, S. T. Rachev & F. J. Fabozzi (2021). Multiple subordinated modeling of asset returns: Implications for option pricing, Econom. Rev., 40 (3), 290-319. DOI: 10.1080/07474938.2020.1781404
Y. Hu, A. Shirvani, W.B. Lindquist, F.J. Fabozzi, S.T. Rachev (2020). Option Pricing Incorporating Factor Dynamics in Complete Markets. J Risk Financial Manag., 13 (12), 321. DOI: https://doi.org/10.3390/jrfm13120321.
A. Shirvani, Y. Hu, S.T. Rachev, and F.J. Fabozzi (2020). Option pricing with mixed Lévy subordinated price process and implied probability weighting function. J. Deriv., 28 (2), 102. DOI: 10.3905/jod.2020.1.102.
A. Shirvani, S.V. Stoyanov, S.T. Rachev, F.J. Fabozzi (2020). A New Set of Financial Instruments, Front. Appl. Math., 6:606812. DOI: 10.3389/fams.2020.606812.
Y. Hu, A. Shirvani, S. Stoyanov, Y.S. Kim, F.J. Fabozzi, and S.T. Rachev (2020). Option Pricing in Markets with Informed Traders, Int. J. Theor. Appl. Finance, 23 (6):2050037. DOI: 10.1142/S0219024920500375
MF is the area of finance in which intricate mathematical models are used to predict markets, set prices, enhance returns, and manage risk.
People
Courses
Academic Publications
Mathematical Finance Program

Mathematical Finance Program
The Department of Mathematics and Statistics at Texas Tech University offers MS and PhD training in mathematical finance. MF is the area of finance in which intricate mathematical models are used to predict markets, set prices, enhance returns, and manage risk. MF professionals are known as quantitative analysts ("quants").
Email Dr. Rachev
zari.rachev@ttu.edu
Email Dr. Lindquist
Brent.Lindquist@ttu.edu
Address
Texas Tech University, 1108 Memorial Circle
Lubbock, TX 79409-1042
Phone
(806) 742-2566
For more information, please contact Dr. Rachev or Dr. Lindquist.
