Mathematical Finance Program
Mathematical Finance M.S. and Ph.D.
Because of the strong demand, admission is highly competitive at both the MS and PhD levels in quantitative finance. The department prepares practitioners who apply mathematical and computational methods to develop and exploit financial opportunities for return enhancement and risk control. The Texas Tech Mathematical Finance program is focused on both risk management (‘beta’ in Wall Street terminology) and ‘alpha generation’ (the Street term for trading strategies for making money). Courses are centered on projects where students use real tick data to analyze and predict the performance of individual stocks and commodities, market indices and derivatives. Texas Tech is one of a few mathematical finance programs offering both MS and PhD training. PhD students of our faculty have taken positions both in Wall Street firms and as faculty in university mathematical finance programs. For more information about our mathematical finance courses and faculty, see MF Graduate Programs and MF People.
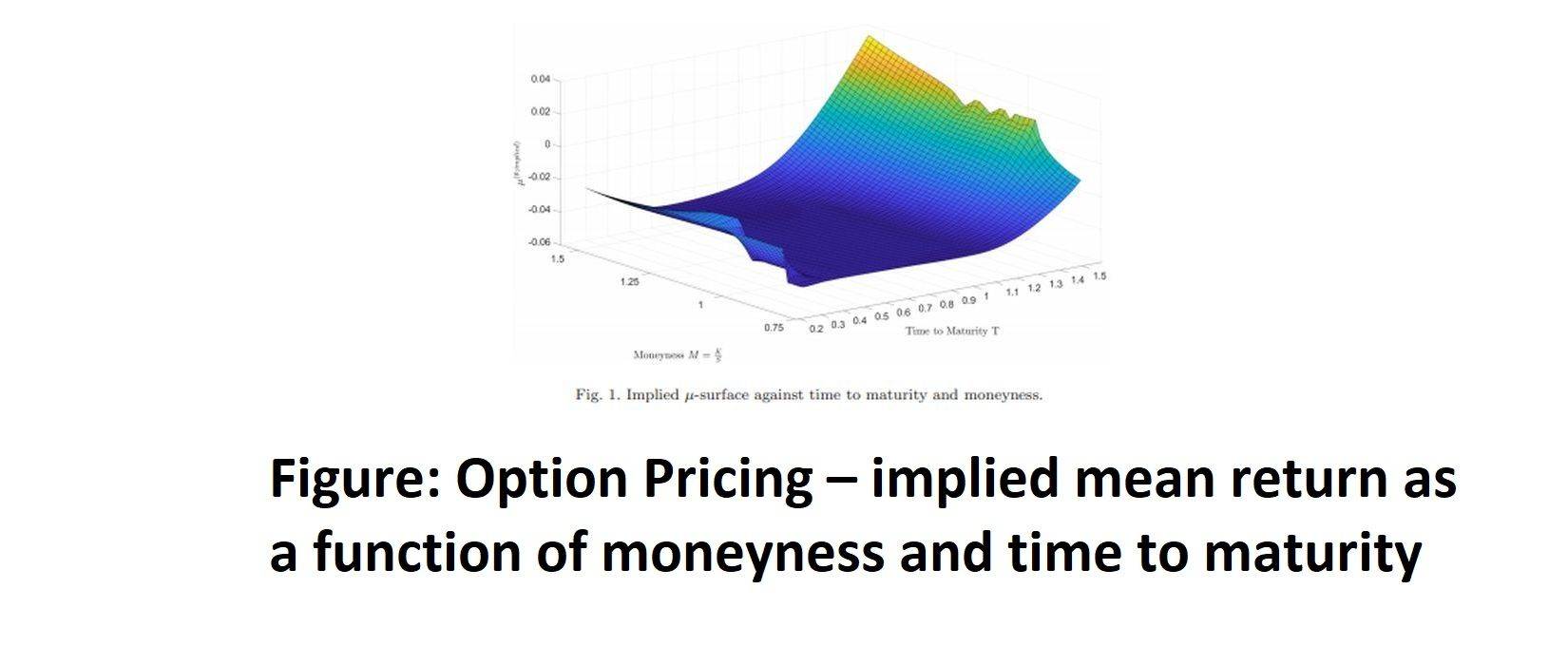
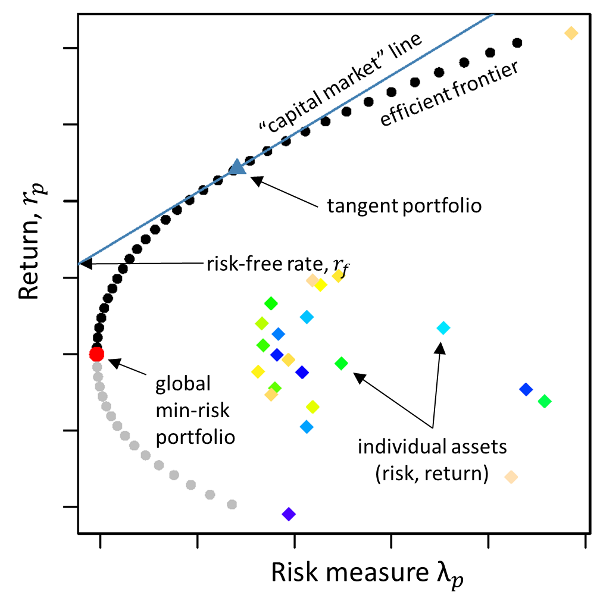
Master of Science with a Specialization in Mathematical Finance
The full-time program of study for the M.S. degree specializing in Mathematical Finance focuses on building a solid foundation in applied mathematics, uncovers models used in financial applications, and teaches computational tools for developing solutions. The M.S. degree consists of 36 hours of graduate work and includes 3 hours of credit for a departmental report or 6 hours of credit for the master’s thesis. Up to 3 hours of graduate work are permitted in other areas such as mathematics, statistics, business, economics, finance, or fields as approved by the graduate advisor. M.S. students share core courses with beginning Ph.D. students.
To enter the program of study leading to a Master of Science Degree specializing in Mathematical Finance, the applicant must meet the requirements of the Graduate School and of the Department of Mathematics and Statistics. The degree requirements are as follows.
Program Contact Information
The Mathematical Finance Program in the Department of Mathematics and Statistics at Texas Tech University is co-directed by Professor Svetlozar (Zari) Rachev, zari.rachev@ttu.edu and Professor W. Brent Lindquist, brent.lindquist@ttu.edu.
For graduate program questions not specifically related to the MF program, contact the Graduate Program Director, Assoc. Prof. Tao (Tom) Lu, t.lu@ttu.edu, or the Graduate Program Coordinator, David Cannon, david.cannon@ttu.edu.
A. Completion of the following required courses.
- FIN 5328 – Options and Futures
- STAT 5328 – Mathematical Statistics I
- STAT 5329 – Mathematical Statistics II
- MATH 5399 (Special Topics) – Applied Time Series
- MATH 6351 – Quantitative Methods with Applications to Financial Data
- MATH 6353 – Stochastic Calculus with Applications to Financial Derivatives
B. Completion of any two courses from the following elective list.
- STAT 5371 – Regression Analysis
- STAT 5386 – Statistical Computation and Simulation
- MATH 6354 – Numerical Partial Differential Equations in Finance
- MATH 6355 – Numerical Methods with Applications to Financial Data
- MATH 6356 – Software Engineering with Financial Applications
- MATH 6357 – Stochastic Processes and Applications to Mathematical Finance
The following electives will appear as special topics from semester to semester:
- MATH 5399 (Special Topics)
- Stochastic Programming, Applications to Asset, Liability, and Wealth Management
- Stochastic Programming for International Portfolio Management
- Computational Methods in Risk Management and Portfolio Optimization
C. Two courses of mathematics to be selected with the approval of the Director of Graduate Studies and the MF program coordinator.
D. Three hours in an area other than mathematical finance, e.g., mathematics, statistics, computer science, economics. This option requires the approval of the appropriate graduate advisor from the selected area.
E. Either:
1. a six-hour Master’s Thesis;
or
2. a three-hour Master’s Report with an additional three-hour course to be selected from requirement B above.
For E.1 an oral thesis defense is required. For E.2 a final comprehensive oral examination on the report is required.
For a brief description of each course, click Course Descriptions.
Master of Science with a Specialization in Mathematical Finance
The full-time program of study for the M.S. degree specializing in Mathematical Finance focuses on building a solid foundation in applied mathematics, uncovers models used in financial applications, and teaches computational tools for developing solutions. The M.S. degree consists of 36 hours of graduate work and includes 3 hours of credit for a departmental report or 6 hours of credit for the master’s thesis. Up to 3 hours of graduate work are permitted in other areas such as mathematics, statistics, business, economics, finance or fields as approved by the graduate advisor. M.S. students share core courses with beginning Ph.D. students.
To enter the program of study leading to a Master of Science Degree specializing in Mathematical Finance, the applicant must meet the requirements of the Graduate School and of the Department of Mathematics and Statistics. The degree requirements are as follows.
- Completion of the following required courses.
- FIN 5328 – Options and Futures
- STAT 5328 – Mathematical Statistics I
- STAT 5329 – Mathematical Statistics II
- MATH 5399 (Special Topics) – Applied Time Series
- MATH 6351 – Quantitative Methods with Applications to Financial Data
- MATH 6353 – Stochastic Calculus with Applications to Financial Derivatives
- Completion of any two courses from the following elective list.
- STAT 5371 – Regression Analysis
- STAT 5386 – Statistical Computation and Simulation
- MATH 6354 – Numerical Partial Differential Equations in Finance
- MATH 6355 – Numerical Methods with Applications to Financial Data
- MATH 6356 – Software Engineering with Financial Applications
- MATH 6357 – Stochastic Processes and Applications to Mathematical Finance
The following electives will appear as special topics from semester to semester
- MATH 5399 (Special Topics)
- Stochastic Programming, Applications to Asset, Liability, and Wealth Management
- Stochastic Programming for International Portfolio Management
- Computational Methods in Risk Management and Portfolio Optimization
- Two courses of mathematics to be selected with the approval of the Director of Graduate Studies and the MF program coordinator.
- Three hours in an area other than mathematical finance, e.g., mathematics, statistics, computer science, economics. This option requires the approval of the appropriate graduate advisor from the selected area.
- Either:
- a six-hour Master’s Thesis;
or
- a three-hour Master’s Report with an additional three-hour course to be selected from requirement B above.
For E.1 an oral thesis defense is required. For E.2 a final comprehensive oral examination on the report is required.
For a brief description of each course, click Course Descriptions.
Typical Course Sequence
The typical course sequence for completion of the M.S. degree with a concentration in MF is as follows.
| First Year – Fall | Cr. | |
| STAT 5328 | Mathematical Statistics I | 3 |
| MATH 6351 | Quantitative Methods with Applications to Financial Data | 3 |
| MATH XXXX | One non-MF math course | 3 |
| First Year – Spring | ||
| STAT 5329 | Mathematical Statistics II | 3 |
| MATH 6353 | Stochastic Calculus with Applications to Financial Derivatives | 3 |
| FIN 5328 | Options and Futures | 3 |
| Second Year – Fall | ||
| MATH 5399 | Applied Time Series | 3 |
| MATH XXXX | MF elective (series B) | 3 |
| MATH XXXX | One non-MF math course | 3 |
| Second Year – Spring | ||
| MATH XXXX | MF elective (series B) | 3 |
| MATH XXXX | MF elective (series B) | 3 |
| MATH 6000 | Master’s report | 3 |
The Ph.D. Degree with a Specialization in Mathematical Finance
The Ph.D. in Mathematics with a specialization in Mathematical Finance is for students seeking careers in research, either ‘on the Street’ or in academia. Doctoral candidates will have a strong affinity for quantitative reasoning and the ability to connect advanced mathematical theories with real-world phenomena. They will have an interest in the creation of complex models and financial instruments as well as a passion for in-depth analysis. Minimum course requirements have been established to ensure that the student obtains a broad background in mathematics and, in addition, attains depth in financial mathematics.
Mathematical Finance Courses
The PhD. degree with a specialization in Mathematical Finance consists of 60 hours of graduate work. The following list is meant to be an outline of minimal requirements. The individual student is encouraged to supplement specified requirements with as much advanced work as possible. Specific course requirement may be waived at the request of the student’s Doctoral Advisory Committee with the consent of the Graduate Program Advisor. Advanced topics seminars which contribute to the student’s overall mathematical background will be offered each semester. It is expected that each student will participate in seminar work in his/her area of specialty. The minimum requirements for coursework are listed below.
- Completion of the following eight required courses.
- FIN 5328 – Options and Futures
- MATH 5322 – Functions of a Real Variable I
- MATH 5323 – Functions of a Real Variable II
- STAT 5328 – Intermediate Mathematical Statistics I
- STAT 5329 – Intermediate Mathematical Statistics II
- MATH 5399 (Special Topics) – Applied Time Series
- MATH 6351 – Quantitative Methods with Applications to Financial Data
- MATH 6353 – Stochastic Calculus with Applications to Financial Derivatives
- Completion of any four courses from the following elective list.
- STAT 5371 – Regression Analysis
- STAT 5380 – Advanced Statistical Methods I
- STAT 5386 – Statistical Computation and Simulation
- STAT 6352 – Bayesian Methods and Application to Financial Data
- MATH 5382 – Advanced Probability I
- MATH 6354 – Numerical Partial Differential Equations in Finance
- MATH 6355 – Numerical Methods with Applications to Financial Data
- MATH 6356 – Software Engineering with Financial Applications
- MATH 6357 – Stochastic Processes and Applications to Mathematical Finance
The following electives will appear as special topics from semester to semester
- MATH 5399 (Special Topics)
- Stochastic Programming, Applications to Asset, Liability, and Wealth Management
- Stochastic Programming for International Portfolio Management
- Computational Methods in Risk Management and Portfolio Optimization
- Twenty-four additional hours selected with the approval of the student’s dissertation advisor and the director of graduate studies. These may include courses offered by the Department of Mathematics and Statistics (excluding STAT 5302-5303 and STAT 5384-5385) relevant to the student’s area of research or courses offered outside the department relevant to the student’s area of research.
- Twelve hours of MATH 8000
A dissertation is required of every candidate for the doctoral degree. This requirement is separate and apart from other requirements in the doctoral program consequently; successful performance in other areas does not necessarily guarantee the acceptance of a dissertation. The dissertation should embody a significant contribution to new information in the subject area.
Preliminary Examinations
The preliminary examinations in Mathematical Finance require knowledge from the following graduate core areas (courses).
- Financial Mathematics (MATH 6351, MATH 6353)
- Probability and Statistics (STAT 5328, STAT 5329)
- One prelim from the pure mathematics sequence
Each examination is four hours long with content based on important fundamental concepts in the area. Each examination is developed by a committee of faculty in the respective core area in consultation with the Graduate Committee. The topics over which a student can be tested are listed in the Preliminary Examination Topics List, which is available from the Graduate Program Advisor. Examples of doctoral preliminary examinations are available on the departmental web page.
Any student who, in four consecutive administrations of the preliminary examinations, does not successfully complete these Examinations may not continue in the doctoral program in the Department of Mathematics and Statistics at Texas Tech University.
Qualifying Examination
Each doctoral student will be required to pass a Qualifying Examination on advanced topics beyond those covered in the Preliminary Examinations. In general, the qualifying examination will follow the format established by the Texas Tech University Graduate Catalog. Any exceptions to this format must be agreed upon by both the student’s Doctoral Advisory Committee and the Graduate Program Advisor.
Departmental Colloquium
Doctoral candidates are expected to present a departmental colloquium prior to graduation.
Final Examination (Ph.D. Defense)
A final public oral examination on the student’s dissertation topics is required of every doctoral candidate
Requirements and Deadlines
Each doctoral student is expected to become familiar with the requirements and deadlines established by the Graduate School and the departments.
Course Descriptions
FIN 5328 – Options and Futures
Focuses on the pricing and use of financial derivative securities and their role in investment management and financial risk management.
MATH 5322 – Functions of a Real Variable I
MATH 5323 – Functions of a Real Variable II
This sequence covers general measure and integration theory, Lp theory, differentiation theory, and basic functional analysis.
MATH 5399 (Special Topics) – Applied Time Series
Stock prices and foreign currency exchange rates are time series. How should we make use of these invaluable data sets to make investment decisions? This course covers applied statistical methodologies pertaining to financial time series especially series of stock price, equity returns, interest rates, and exchange rates, with an emphasis on model building and accurate prediction. The course introduces techniques involved with forecasting key variables and how to incorporate model uncertainty into financial forecasts.
MATH 5382 – Advanced Probability I
Measure and integration, axiomatic foundations of probability theory, random variables, distributions and their characteristic functions, stable and infinitely divisible laws, limit theorems for sums of independent random variables, conditioning, Martingales.
MATH 6351 – Quantitative Methods with Applications to Financial Data
Coverage of important topics in modern mathematical finance at the graduate level. The emphasis is on: general principles of modelling the price dynamics of financial assets; quantitative techniques; behavioral finance; market risk and other types of financial risks; volatility modeling; and the foundations of high-frequency arbitrage trading. The topics covered will enable the student to develop the theoretical knowledge and practical skills required for successfully handling multiple types of risks in modern financial markets.
MATH 6353 – Stochastic Calculus with Applications to Financial Derivatives
The mathematical foundation for understanding modern financial theory, starting with general probability theory and leading to basic results in pricing exotic and American derivatives. The course covers: filtrations and generalized conditional expectation; the Girsanov theorem and the Radon-Nikodym process; martingales; Brownian motion; Ito integration and processes; the Black-Scholes formula; risk neutral pricing and the Feynman-Kac theorem. Applications to financial instruments are discussed throughout.
MATH 6354 – Numerical Partial Differential Equations in Finance
Basic introduction into the valuation of financial options via the numerical solution of partial differential equations (PDEs). The course covers the main concepts, models, methods and results that arise in the numerical approach. The focus begins with one-dimensional financial PDEs, notably the Black-Scholes equation, and continues with a detailed discussion of the important step towards two-dimensional PDEs in finance.
MATH 6355 – Numerical Methods with Applications to Financial Data
A large class of problems cannot be analyzed with analytical tools; numerical methods are especially vital in all areas of modern finance. To learn how to use computational tools in an informed and intelligent way, this course endeavors to explain not only when and how to use various numerical algorithms but also how and why they work. This course offers an introduction to numerical analysis and quantitative finance applications. The techniques presented in this course are applicable to a wide range of financial fields (options, simulation, fixed income valuation). Special attention will also be paid to financial applications of analytic and numerical optimization, covering the different types of optimization problems.
MATH 6356 – Software Engineering with Financial Applications
Essential C++ topics with applications to finance. The course focuses on numerical analysis and quantitative finance applications.
MATH 6357 – Stochastic Processes and Applications to Mathematical Finance
Basic introduction to probability theory and stochastic processes for financial applications. The course discusses modelling financial markets with stochastic processes, including the famous Black–Scholes–Merton (BSM) model. It introduces the pertinent mathematical concepts of ‘predictability’ in application to investment portfolios and hedging strategies, and martingales and martingale measures in application to the concepts of efficiency and absence of arbitrage in financial markets. Lévy models, which improve on the performance of BSM, are introduced to take account of different stylized features of the markets. The pricing of derivative securities in market models based on Lévy processes is also covered.
The following electives will appear as special topics from semester to semester.
MATH 5399 (Special Topics)
- Financial Software Engineering
Need Description
- Stochastic Programming, Applications to Asset, Liability, and Wealth Management
Introduction to stochastic programming for asset and liability management. The theory of multistage stochastic programming, focusing on problem formulation, mathematical properties and solution methods. Applications of stochastic programming models for various types of investors, including insurance companies, pension funds, individuals, and hedge funds. During the course a multistage stochastic programming model for a specific financial application will be implemented in a programming language.
- Stochastic Programming for International Portfolio Management
Introduction to stochastic programming models for international portfolio management. Mathematical properties and solution techniques of multistage stochastic programming models presented along with financial applications such as derivative pricing and portfolio optimization. Emphasis given to model portfolios with derivative contracts to control market and currency risks.
- Computational Methods in Risk Management and Portfolio Optimization
Need Description
STAT 5328 – Intermediate Mathematical Statistics I
Probability spaces, continuous and discrete distributions, functions of random variables, expectation, conditional expectation, central limit theorem, convergence concepts, order statistics, sampling distributions.
STAT 5329 – Intermediate Mathematical Statistics II
Sufficiency and completeness, information, estimation, maximum likelihood, confidence intervals, uniformly most powerful tests, likelihood ratio tests, normal based inference, Bayesian inference.
STAT 5371 – Regression Analysis
Estimation and testing in linear regression, residual analysis, influence diagnostics, multicollinearity logistic regression, nonlinear regression.
STAT 5380 – Advanced Statistical Methods I
Theory of estimation and tests of statistical hypotheses, sequential analysis.
STAT 5386 – Statistical Computation and Simulation
Basics of computing, optimization methods, EM algorithm, simulation of random variables, Monte Carlo methods, Markov Chain Monte Carlo, additional topics (time permitting).
STAT 6352 – Bayesian Methods and Application to Financial Data
Detailed overview of the theory of Bayesian methods and their applications to financial modeling.
MF is the area of finance in which intricate mathematical models are used to predict markets, set prices, enhance returns, and manage risk.
People
Courses
Academic Publications
Mathematical Finance Program

Mathematical Finance Program
The Department of Mathematics and Statistics at Texas Tech University offers MS and PhD training in mathematical finance. MF is the area of finance in which intricate mathematical models are used to predict markets, set prices, enhance returns, and manage risk. MF professionals are known as quantitative analysts ("quants").
Email Dr. Rachev
zari.rachev@ttu.edu
Email Dr. Lindquist
Brent.Lindquist@ttu.edu
Address
Texas Tech University, 1108 Memorial Circle
Lubbock, TX 79409-1042
Phone
(806) 742-2566
For more information, please contact Dr. Rachev or Dr. Lindquist.
