PROGRAM SCHEDULE - XIX RED RAIDER MINI-SYMPOSIUM
DIFFERENTIAL GEOMETRY AND INTEGRABLE SYSTEMS
The following is a tentative program schedule for the XIX Red Raider Mini-Symposium. Please check back here for the most up-to-date information.
Thursday Schedule - TLPDC Rm 151 located in Texas Tech Library
| Thursday Hours | Speaker | Title | Abstract |
|---|---|---|---|
| 8:30 am - 9.00 am | Morning Snack | ||
| 9.00 am - 9.30 am | Opening/Registration Dean Dupras Opening Remarks |
||
| 9.30 am - 10.30 am | Xialong Li | Curvature operator of the second kind | The Riemann curvature tensor on a Riemannian manifold induces two kinds of curvature operators: the first kind acting on two-forms and the second kind acting on symmetric two-tensors. The curvature operator of the second kind recently attracted a lot of attention due to the resolution of Nishikawa's conjecture by Cao-Gursky-Tran. In this talk, I will survey recent works on understanding the curvature operator of the second kind on Riemannian and K\"ahler manifolds and also mention some interesting problems. |
| 10.30 am - 11.30 am | Rafael Lopez | Some themes around the notion of catenary | The catenary is the shape of a hanging chain suspended from its endpoints. In this talk, we will give some topics around the catenary curve, such as its extension to higher dimensions and the study of catenaries in other ambient spaces. As a special interest, we focus on the axisymmetric singular minimal surfaces, which are models of domes and roofs. We will discuss if catenary rotation surfaces and paraboids can be candidates for models of domes. |
| 11.30 am - 12.00 pm | Break | ||
| 12.00 pm - 1.00 pm | Ailana Fraser | Stable minimal surfaces and applications | I will discuss questions about stable minimal surfaces in Euclidean space and Riemannian manifolds, and give new perspectives and new results about manifolds with positive isotropic curvature. |
| 1.00 pm - 2:30 pm | Lunch Break | ||
| 2:30 pm - 3:30 pm | Nicola Garofalo (SIAM Colloquium) Location - Escondido Theater in SUB |
The restriction problem for the Fourier transform | The Fourier transform is one of the most fundamental tools in classical analysis. It plays a pervasive role in several branches of theoretical mathematics and of the applied sciences. The theorem of Hausdorff-Young states that, when p is an exponent in the interval [1,2], the Fourier transform of a function in the Lebesgue class L^p belongs to the dual Lebesgue space L^p’. As such, it is only defined almost everywhere and therefore it is a priori all but clear why it should be possible to restrict it to a lower dimensional manifold, such for instance the unit sphere, which has zero Lebesgue measure. The restriction conjecture states that this is in fact possible, provided that p stays in a certain optimal subinterval of the Hausdorff-Young range [1,2]. I will give a completely self-contained presentation of such conjecture, and hint at the role that the curvature (of the sphere) plays in it. I will also highlight the celebrated Tomas-Stein theorem which completely solves the restriction problem when the target is L^2 of the unit sphere. If time permits, some notable applications will be given. Disclaimer: although it is helpful to know a bit of Lebesgue spaces, to enjoy this talk you do not need to know much about them. I will tell you the very basics. |
| 4.00 pm - 5.00 pm | Donatella Danielli | Obstacle problems for fractional powers of the Laplacian | In this talk we will discuss a sampler of obstacle-type problems associated with the fractional Laplacian $(-\Delta)^s$ , for $1 < s < 2$. Our goals are to establish regularity properties of the solution and to describe the structure of the free boundary. To this end, we combine classical techniques from potential theory and the calculus of variations with more modern methods, such as the localization of the operator and monotonicity formulas. This is joint work with A. Haj Ali (Arizona State University) and A. Petrosyan (Purdue University). |
| 5.30 pm - 7.00 pm | Dinner Reception - Math Room 238 | ||
Friday Schedule - TLPDC Rm 151 located in Texas Tech Library
| Friday Hours | Speaker | Title | Abstract |
|---|---|---|---|
| 9.00 am - 9.30 am | Morning Snack | ||
| 9.30 am - 10.30 am | Wayne Rossman | Surface theory, from Weierstrass representations to Lie sphere geometry | Weierstrass representations provide explicit tools for constructing and examining very particular classes of surfaces, such as minimal surfaces in Euclidean 3-space, flat surfaces and constant mean curvature 1 surfaces in hyperbolic 3-space, and maximal surfaces in Lorentz 3-space. There are also generalizations, such as the DPW method of Dorfmeister, Pedit and Wu, using more complex integrable systems structure but still allowing for constructions that are explicit in some sense. This method produces harmonic maps, and in particular produces general constant mean curvature surfaces in Euclidean 3-space. It is useful to consider such constructions from the viewpoint of transformation theory, for many reasons, three of which I aim to touch on in this talk: 1) it allows for extension of the ideas used in Weierstrass representations to much more general classes of surfaces, 2) it allows for unified approaches where different classes of surfaces can be seen as the same, in the context of Moebius geometry or Lie sphere geometry, 3) it indicates how to develop a theory of discrete surfaces, complete with curvature properties, Weierstrass representations, and more. |
| 10.30 am - 11.30 am | Franz Pedit | Minimal Lagrangian surfaces of high genus in $CP^2$ | I will explain how to construct examples of high genus minimal Lagrangian surfaces in $CP^2$ using a combination of methods from integrable systems, loop group factorization, and Higgs bundles. The talk is based on joint work with S. Heller and C. Ouyang. |
| 11.30 am - 12.00 pm | Break | ||
| 12.00 pm - 1.00 pm | Matthew Gursky | The ASD deformation complex and a conjecture of Singer | In this talk I will give a brief overview of the deformation complex for anti-self-dual 4-manifolds, and formulate a conjecture (attributed to Singer) about the vanishing of one of the cohomology groups. I will then report on some recent progress on resolving this conjecture. This is joint work with Rod Gover. |
| 1.00 pm - 3.00 pm | Lunch Break | ||
| 3.00 pm - 4.00 pm | Francesco Bullo | Contraction Theory in Systems and Control | We survey a comprehensive theory on the application of the Banach contraction principle to control and dynamical systems. We start with some historical highlights. Next, we generalize the basic contraction property from discrete to continuous time, from Euclidean to non-Euclidean norms, from closed to open systems, and, finally, from single to interconnected systems. We then apply these theoretical tools to modern problems involving machine learning, multi-agent coordination, and optimal control. Finally, we conclude with strengths and weaknesses of the theory as well as open directions of research. |
| 4.00 pm - 5.00 pm | Gaetano Napoli | Nematic shells: soft matter meets surface geometry | Nematic ordering on curved surfaces provides an excellent laboratory in which current topics in condensed matter physics meet methods and concepts from geometry and mathematical analysis. The typical problem in statics of nematic liquid crystals is to determine the nematic alignment (represented by vector or tensor fields) in a given spatial region as a stationary point of an energy functional defined over this domain. When the occupied region is extremely thin, it can be considered as a surface. Consequently, the problem can be reformulated as: determine a field of directions tangent to the surface, by minimising an effective surface potential. In this talk, I discuss some surface models consistent with the classical vector (Frank) and tensor (Landau-de Gennes) theories of 3D liquid crystals. The reduction from 3D to effective 2D models highlights the interplay between the nematic order parameter (whether vector or tensor) and the geometry of the underlying surface. Within the framework of 2D vector theory, I illustrate some simple examples of effects induced by the extrinsic curvature on the nematic alignment. I also discuss a generalized Plateau-like problem, where the surface and the nematic texture influence each other. In the context of 2D tensor theory, I address the problem of nematic texture tangent to a spherical surface and the location of topological defects (melting points). |
Saturday Schedule - Carlsbad Caverns in Carlsbad, NM




Carlsbad Caverns is a natural wonder located in the Guadalupe Mountains in southeastern New Mexico, United States.
It is a complex of 119 limestone caves, the largest of which is called the Big Room, and is known for its impressive array of stalactites, stalagmites, and other unique rock formations.
The Caverns are a popular tourist destination and offer a variety of tours and attractions for visitors, including guided tours of the caves, hiking trails, and a bat flight program.
Carlsbad Caverns is also a designated UNESCO World Heritage Site and is protected as a national park by the U.S. National Park Service. Click here to go to the website that provides comprehensive information regarding the Caverns.
| Saturday Hours | Activities |
|---|---|
| 7.00 am - 8.00 am | Leaving for Carlsbad Carverns |
| 10.30 am - 11.00 am | Arriving at Carlsbad caverns |
| 11.00 am - 12.00 pm | Lunch |
| 12.00 pm - 4.00 pm | Exploring Caverns |
| 4.00 pm - 4.30 pm | Leaving Carlsbad Caverns |
| 8.30 pm - 9.00 pm | Arriving back in Lubbock |
Sunday Schedule - Math Rm 108
| Sunday Hours | Speaker | Title | Abstract |
|---|---|---|---|
| 8:30 am - 9.00 am | Morning Snack | ||
| 9.00 am - 10.00 am | Dan Knopf | Singularity formation of complete Ricci flow solutions | We study a class of noncompact Ricci flow solutions that form singularities at spatial infinity. We will discuss methods useful for their analysis and a condition conjecturally sufficient to obtain nontrivial shrinking solitons as singularity model limits of blowup sequences in noncompact solutions. The talk will be suitable for a general audience. |
| 10.00 am - 11.00 am | Jonathan Zhu | Distance comparison principles for curve shortening flows | For closed curves evolving by their curvature, the theorem of Gage-Hamilton and Grayson establishes that an embedded curve contracts to a round point. An efficient proof was later found by Huisken, with improvements by Andrews-Bryan, which uses multi-point maximum principle techniques. We’ll discuss the use of these techniques in other settings, particularly for the long-time behaviour of curve shortening flow with free boundary. |
| 11.00 am - 11.30 pm | Break | ||
| 11:30 pm - 12.30 pm | Rob Kusner | Eigenspaces and Minimal Surfaces | Sharp dimension bounds for (Steklov and Laplacian) eigenspaces on Riemannian surfaces are used to study existence and classification problems for embedded minimal surfaces (free boundary surfaces in the round ball, and closed minimal surfaces in the round sphere. |
| 12.30 pm - 2.30 pm | Conclusion | ||
Program Schedule - Location
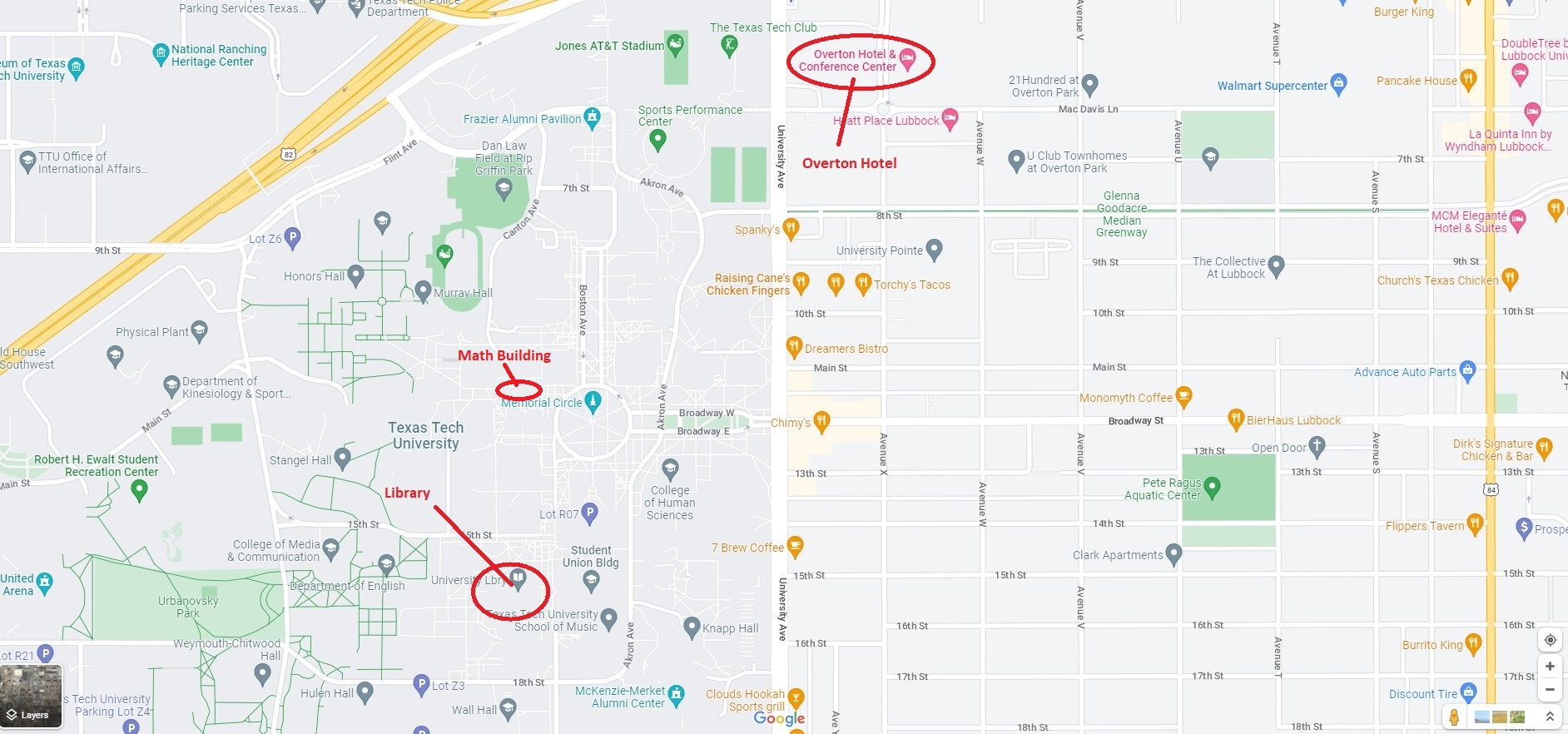
Thursday's and Friday's talks will be held in the TLPDC Room 151 located inside the Texas Tech Library. Sunday's talks will be held in Room 108 inside the Math Building. In order to help participants locate each room, please see this map which shows the direction from Overton Hotel. For further clarity, see the map below (which has the Library highlighted).