Linear Problems
The information required to specify a linear PDE can be aggregated into a LinearProblem object. Aspects of using the LinearProblem object are described on this page
- Creating a Linear Problem
- Solving a Linear Problem
- Ordering of Equations and Unknowns
- Access to Low-Level Problem Information
Creating a Linear Problem
The LinearProblem constructor takes six arguments,- A Mesh, specifying the discrete geometry on which the problem is to be solved.
- An Expr specifying the weak form of the equations
- An Expr specifying the essential boundary conditions (if any). If the problem has no essential boundary conditions, then an empty expression should be given for this argument.
- An Expr listing the test functions appearing in the equations. If there are multiple test functions, they should be passed through a List operator.
- An Expr listing the unknown functions appearing in the equations. If there are multiple unknowns, they should be passed through a List operator.
- A TSFExtended::VectorType<double> object, specifying the type of low-level linear algebra objects to be used.
Specifying Multiple Equations and Unknowns
Sundance can handle an arbitrarily large number of coupled weak equations and unknown field variables. Multiple weak equations can be written in two equivalent ways: as a List of equations, or as a sum of integrals. Because each equation is written in terms of its own test function, and the test functions are linearly independent, a sum of two weak equations is equivalent to enumerating the two equations in a list.For example, consider solving the coupled system of equations
![\[ u_{xx} = v \]](form_59.png)
![\[ v_{xx} = 1 \]](form_60.png)
on ![$\Omega \equiv x \in [0,1]$](form_61.png) with boundary conditions
with boundary conditions
![\[ u(0)=u(1)=0 \]](form_62.png)
![\[ v(0)=v(1)=0 \]](form_63.png)
The Galerkin weak form of the equation is
![\[ \int_\Omega u_x {\hat u}_x + {\hat u} v + \int_\Omega v_x {\hat v}_x + x {\hat v} = 0 \;\; \forall {\hat u}, {\hat v} \]](form_64.png)
We can write the pieces of this weak form in Sundance code as
Expr uEqn = Integral(interior, (dx*uHat)*(dx*u) + uHat*v, quad2); Expr vEqn = Integral(interior, (dx*vHat)*(dx*v) + x*vHat, quad2);
uEqn + vEqn or List(uEqn, vEqn). Likewise, the essential BCs can either be added or listed. Internally, a list of equations in transformed into a sum so the difference is purely one of taste at the user level.Solving a Linear Problem
A LinearProblem assembles the matrix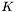 and vector
and vector 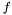 that appear in the discrete form of the linear problem
that appear in the discrete form of the linear problem
![\[ K x = f \]](form_65.png)
To solve this system, a linear solver algorithm is required. See the section on linear solvers for information on setting up linear solvers.
A linear problem is most easily solved using the solve() method of LinearProblem, for example,
Expr soln = myProb.solve(mySolver);
mySolver is an object of type TSFExtended::LinearSolver. As can be seen, the solution is returned as a Sundance expression object, and thus can be used in other equations.Checking the Solve Status
After solving, the convergence status of the solver can be obtained by calling the LinearProblem::solveStatus() method.Ordering of Equations and Unknowns
The order in which equations and unknowns are written can make a difference in the performance of a linear solver, and in keeping with the overall design goal of flexibility, Sundance gives you the ability to specify this ordering. In order to understand how Sundance's ordering specification works, let's look into how Sundance decides unknown and equation numbering.Given a mesh and a set of unknowns, the Sundance discretization engine will traverse the mesh one maximal cell at a time and find all unknowns associated with that cell and its facets. In a problem with multiple unknowns, say velocity, pressure, and temperature, there can be more than one unknown associated with a cell; if so, the unknowns are assigned in the order that their associated UnknownFunction objects are listed in the LinearProblem constructor. This scheme gives us two ways to control the unknown ordering:
- Cell ordering specifies the order in which cells are encountered as the mesh is traversed.
- Function ordering specifies the order in which different functions are listed within a single cell.
Ordering of Cells
There are low-level hooks for alternate cell orderings in Sundance, however, at this point we have only implemented the identity reordering, i.e., no reordering relative to the ordering defined by the mesh.Ordering of Functions
Function ordering is controlled by the order in which test or unknown functions appear in the linear problem constructor. For example, ifux, uy, and p are unknowns we can order them as List(ux, uy, p), or as List(p, ux, uy) or any of the other permutations. A list with the desired ordering is given to the LinearProblem constructor, e.g., Notice that the test functions need not have the same ordering as their corresponding unknowns: it is possible to do a nonsymmetric ordering such as Nonsymmetric reorderings are often useful in PDE-constrained optimization.Segregation of Equations and Unknowns into Blocks
Segregation of variables is not yet implemented in this version of Sundance.Access to Low-Level Problem Information
Programming with Sundance is usually done at a high level of abstraction; however, it is sometimes useful to get low-level information about the discrete form of a problem.Access to Operators and Vectors
If you want to inspect the system matrix and vector, or want to use them for some purpose other than solving a linear system, it is possible to do so. ThegetOperator() and getRHS() methods of LinearProblem return the stiffness matrix and load vector, respectively. They are returned as TSF objects. You may sometimes want to access the concrete object referenced by a TSF object; if so, refer to the documentation for the TSF adaptors to your concrete type for details on how to extract the concrete object, e.g., an EPetra matrix, underlying a TSF object.DOF Maps and Essential BC Markers
The degree-of-freedom (DOF) maps for the row and column spaces can be accessed through the rowMap() and colMap() methods of LinearProblem. These maps specify how cell and function indices are mapped into indices into the matrix and vector. This is sometimes useful for low-level debugging, or for making custom modifications to your matrix or vector.The bcRows() method of LinearProblem returns an STL set of all rows that are marked as boundary condition rows and processed using the replace method described in the page on boundary conditions.


