Boundary Conditions
There are many ways to apply boundary conditions in a finite element simulation. To begin with, the way a boundary condition gets written depends strongly on the way the weak problem has been formulated; for instance, boundary conditions will be written quite differently in least-squares formulations than in Galerkin formulations. In this documentation we describe how to apply BCs in a Galerkin formulation.Specifying where a boundary condition gets applied
In Sundance, geometric subdomains are identified using CellFilter objects. The surface on which a BC is to be applied is specified by passing as an argument the CellFilter representing that surface.Nonlinear Boundary Conditions
Some problems will have nonlinear boundary conditions, for example in radiative heat transfer from a convex surface the heat flux is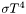 where
where 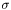 is the Stefan-Boltzmann constant. Sundance requires you to handle nonlinear BCs in the same way you handle nonlinear PDEs: by iterative solution of a linearized problem. The linearization will depend on the iterative method used.
is the Stefan-Boltzmann constant. Sundance requires you to handle nonlinear BCs in the same way you handle nonlinear PDEs: by iterative solution of a linearized problem. The linearization will depend on the iterative method used.It is important to realize that a linear PDE with nonlinear BCs gives rise to a nonlinear problem, the linearity of the PDE notwithstanding.
BCs for Galerkin and Petrov-Galerkin Formulations
In a Galerkin or Petrov-Galerkin formulation, integration by parts yields boundary terms involving a test function and the derivative of an unknown function. The trick to doing BCs is to figure out how to build the BCs into this surface term.Neumann Boundary Conditions
Neumann BCs specify the value of a normal derivative, or some combination of derivatives, along a boundary surface. They arise in problems where a flux has been specified on a boundary; for example, a heat flux in heat transfer or a surface traction (momentum flux) in solid mechanics. An important and quite common special case is a homogeneous Neumann BC, where the boundary flux is zero; examples are insulating surfaces in heat transfer and free surfaces in solid mechanics. Homogeneous Neumann BCs are often called natural BCs in the finite elements literature, and they have a particularly simple representation.Writing Neumann BCs in Galerkin formulations is extremely simple. After integration by parts, we will have boundary terms involving test functions times derivatives of our unknowns. To apply a Neumann BC, we simply replace the derivatives appearing in those boundary terms with their value determined by the BC. Homogeneous Neumann BCs are a particularly simple special case because the boundary integrals go to zero, letting us satisfy the BC by simply ignoring the boundary integrals on those regions! It doesn't get much simpler than that.
Robin Boundary Conditions
Robin BCs, often called boundary conditions of the third kind, specify a linear combination of a field value and its normal derivative. Robin BCs occur, for example, on a surface from which heat is carried by convection. Robin BCs are handled similarly to Neumann BCs, in that we replace the derivative in a surface term with its value computed from the BC; however, with a Robin BC we replace the derivative with a linear expression involving the unknown field rather than with a known expression.Dirichlet Boundary Conditions
Dirichlet boundary conditions specify the value of a field on a boundary segment. Some physical examples are specifying the temperature on a surface that is in contact with a heat bath, or specifying that a viscous fluid ``sticks'' to a surface.In many cases we can enforce Dirichlet boundary conditions on certain nodes or edges by replacing the PDE at those entities with an equation representing the Dirichlet BCs. This can be done nodewise or weakly over the boundary cell; note that nodewise BC application is a special case of weak BC application obtained by using a nodal quadrature rule. A justification of this scheme is given below in section Optional: More about Dirichlet BCs.
In Sundance we write such a boundary condition using the EssentialBC object. The most general constructor for an EssentialBC takes as arguments
- the CellFilter on which the BC is to be applied
- a weak form of the BC.
- a QuadratureFamily
Example: BCs for Laplace's Equation
We now show how to write Neumann, Robin, and Dirichlet boundary conditions for the Laplace equation in Sundance. The equation on the interior of the domain is
![\[ \nabla^2 u = 0 \; \mathrm{in} \; \Omega. \]](form_7.png)
On the boundary regions 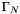 ,
, 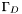 , and
, and 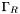 we have boundary conditions
we have boundary conditions
![\[ \frac{\partial u}{\partial n} = G \]](form_11.png)
![\[ u = u_D \]](form_12.png)
![\[ \frac{\partial u}{\partial n} = \alpha (u - u_R) \]](form_13.png)
We form a weak equation by multiplying by a test function 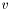 and integrating, giving
and integrating, giving
![\[ - \int_\Omega \nabla v \cdot \nabla u + \int_\Gamma v \frac{\partial u}{\partial n} = 0 \]](form_15.png)
which must hold for all 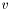 in a suitable subspace. On the Neumann and Robin regions, we can substitute
in a suitable subspace. On the Neumann and Robin regions, we can substitute 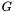 and
and 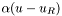 , respectively, for the normal derivative
, respectively, for the normal derivative 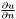 , so that these BCs are simply included in the weak form as written. The method for applying Dirichlet BCs is described in Optional: More about Dirichlet BCs.
, so that these BCs are simply included in the weak form as written. The method for applying Dirichlet BCs is described in Optional: More about Dirichlet BCs.
This equation is written in Sundance with code such as the following
// Define test and unknown functions Expr v = new TestFunction(some basis); Expr u = new UnknownFunction(some basis); // Define a cell filter for the interior of the region CellFilter omega = new MaximalCellFilter(); // Define cell filters for the surfaces on which // neumann, robin, and dirichlet are to be applied. CellFilter gamma_neumann = [some cell filter definition]; CellFilter gamma_robin = [some other cell filter definition]; CellFilter gamma_diri = [yet another cell filter definition]; // Define an expression for the flux on the Neumann surface Expr G = [some expression]; // Define expressions for the variables in the Robin BC Expr alpha = [some expression]; Expr u_R = [some other expression]; // Define expressions for the variable in the Dirichlet BC Expr u_D = [some expression]; Expr eqn = Integral(omega, (grad*v)*(grad*u)) + Integral(gamma_neumann, v*G) + Integral(gamma_robin, v*alpha*(u-u_R)); Expr essBC = EssentialBC(gamma_diri, v*(u-u_D));
Optional: More about Dirichlet BCs
The replacement scheme for Dirichlet boundary conditions described above may seem ad-hoc, however it can be given a sound mathematical foundation as a limit of a Robin boundary condition.
Without loss of generality, we'll use as a model problem the Laplace equation with Dirichlet conditions 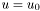 on the entire boundary:
on the entire boundary:
![\[ \nabla^2 u = 0 \; \mathrm{in} \; \Omega \]](form_20.png)
![\[ u=u_0 \; \mathrm{on} \; \Gamma. \]](form_21.png)
As usual, we form a weak equation by multiplying by a test function 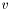 and integrating, giving
and integrating, giving
![\[ - \int_\Omega \nabla v \cdot \nabla u + \int_\Gamma v \frac{\partial u}{\partial n} = 0 \]](form_15.png)
which must hold for all 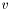 in a suitable subspace. We now impose a Robin boundary condition
in a suitable subspace. We now impose a Robin boundary condition
![\[ \epsilon \frac{\partial u}{\partial n} = u - u_0, \]](form_22.png)
which in the limit 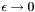 approaches the Dirichlet condition
approaches the Dirichlet condition 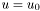 . With this BC, the weak equation becomes
. With this BC, the weak equation becomes
![\[ - \int_\Omega \nabla v \cdot \nabla u + \frac{1}{\epsilon}\int_\Gamma v \left(u - u_0\right) = 0 \]](form_24.png)
At this point, we could simply take a small but nonzero 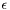 and solve the problem. This is equivalent to a penalty method for imposing the BC, and unfortunately leads to poorly conditioned linear systems. We want to do better, and take the limit
and solve the problem. This is equivalent to a penalty method for imposing the BC, and unfortunately leads to poorly conditioned linear systems. We want to do better, and take the limit 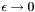 so that the Dirichlet BC is satisfied exactly, yet we also want to avoid ill-conditioning. As we will show, we can often have it both ways, taking the limit without ill-conditioning, but the argument must be developed carefully because the way in which that limit is taken is important.
so that the Dirichlet BC is satisfied exactly, yet we also want to avoid ill-conditioning. As we will show, we can often have it both ways, taking the limit without ill-conditioning, but the argument must be developed carefully because the way in which that limit is taken is important.
We will discretize the system before taking the limit. We expand 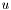 in a series of basis functions,
in a series of basis functions,
![\[ u(x) = \sum_j u_j \phi_j(x) \]](form_27.png)
and evaluate Blah} with each member of 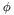 as test functions. The discrete equations are
as test functions. The discrete equations are
![\[ \left[{\bf A} + \frac{1}{\epsilon} {\bf B}\right] \cdot {\bf u} = \frac{1}{\epsilon} {\bf B} \cdot {\bf u}_0 \]](form_29.png)
where the matrices are defined as
![\[ {\bf A}_{ij} = -\int_\Omega k \nabla\phi_i \cdot \nabla \phi_j \]](form_30.png)
![\[ {\bf B}_{ij} = \int_{\Gamma} \phi_i \phi_j \]](form_31.png)
At this point we make a critical assumption: that we are using either Lagrange or Serendipity basis functions. These basis functions are { nodal}, by which we mean we can make an association between basis functions and mesh nodes, and then define the basis functions in such a way that the 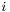 -th basis function
-th basis function 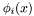 is zero at every node but the
is zero at every node but the 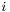 -th. Furthermore, these basis sets have the important property that { only those basis functions
-th. Furthermore, these basis sets have the important property that { only those basis functions 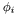 associated with nodes on the surface
associated with nodes on the surface 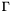 have nonzero values on the surface
have nonzero values on the surface 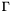 .} We can now partition the equations and variables according to whether each row or column is associated with a node on
.} We can now partition the equations and variables according to whether each row or column is associated with a node on 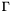 . Notice that the dangerous denominator appears only in terms involving
. Notice that the dangerous denominator appears only in terms involving 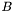 , whose elements are obtained by integrating over
, whose elements are obtained by integrating over 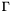 . Thus all elements of
. Thus all elements of 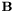 involving nodes not on
involving nodes not on 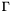 are zero. Marking elements associated with
are zero. Marking elements associated with 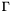 with the superscript
with the superscript 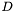 and all others with the superscript
and all others with the superscript 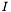 , we can write each matrix as a block matrix, e.g.,
, we can write each matrix as a block matrix, e.g.,
![\[ {\bf A} = \left[ \begin{array}{cc} {\bf A}^{II} & {\bf A}^{ID} \\ {\bf A}^{DI} & {\bf A}^{DD} \end{array}\right]. \]](form_40.png)
In particular, from the argument above we know that all off-boundary elements of 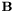 are zero,
are zero,
![\[ {\bf B} = \left[ \begin{array}{cc} {\bf 0} & {\bf 0} \\ {\bf 0} & {\bf B}^{DD} \end{array} \right]. \]](form_41.png)
With this notation, we can write out the system,
![\[ \left[\begin{array}{cc} {\bf A}^{II} & {\bf A}^{ID} \\ {\bf A}^{DI} & {\bf A}^{DD} + \frac{1}{\epsilon} {\bf B} \end{array} \right] \left[ \begin{array}{c} {\bf u}^I \\ {\bf u}^D \end{array} \right] = \left[ \begin{array}{c} {\bf 0} \\ \frac{1}{\epsilon}{\bf B}\cdot {\bf u_0} \end{array} \right] \]](form_42.png)
Multiplying the second row by $$ removes the explosive denominator
![\[ \left[ \begin{array}{cc} {\bf A}^{II} & {\bf A}^{ID} \\ \epsilon {\bf A}^{DI} & \epsilon {\bf A}^{DD} + {\bf B} \end{array} \right] \left[ \begin{array}{c} {\bf u}^I \\ {\bf u}^D \end{array}\right] = \left[ \begin{array}{c} {\bf 0} \\ {\bf B}\cdot {\bf u_0} \end{array}\right] \]](form_43.png)
so that it is safe to take the limit $ 0$, yielding the well-behaved system
![\[ \left[ \begin{array}{cc} {\bf A}^{II} & {\bf A}^{ID} \\ {\bf 0} & {\bf B} \end{array} \right] \left[ \begin{array}{c} {\bf u}^I \\ {\bf u}^D \end{array}\right] = \left[ \begin{array}{c} {\bf 0} \\ {\bf B}\cdot {\bf u_0} \end{array}\right] \]](form_44.png)
This entire process can be summarized as such: for surfaces on which Dirichlet BCs apply, we simply replace all equations by the Dirichlet boundary term. The bookkeeping for this would be daunting if we had to keep track of off-boundary and on-boundary nodes in the equation specification. However, in Sundance the specification that a term is to be handled in this special way via replacement (or more precisely via limit and rescaling) is done by putting the term inside an EssentialBC object rather than an Integral object. The Sundance computational kernel will figure out which rows get replaced and rescaled.
Discontinous Dirichlet BCs
It is not uncommon to encounter boundary conditions in which a field is set to a function that is discontinuous. An example is the lid-driven cavity problem of fluid mechanics, in which the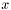 -component of velocity is zero along the side walls and nonzero along the top lid. The
-component of velocity is zero along the side walls and nonzero along the top lid. The 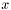 velocity is discountinuous at the two top corners, and it is necessary to choose a scheme for assigning the boundary value at the points of discontinuity. Several ideas suggest themselves:
velocity is discountinuous at the two top corners, and it is necessary to choose a scheme for assigning the boundary value at the points of discontinuity. Several ideas suggest themselves:
- Pick one of the two boundary conditions and apply it at the corner point.
- Average the two boundary conditions.
Nonlocal Boundary Conditions
Nonlocal boundary conditions arise naturally in problems such as radiative heat transfer from non-convex surfaces, and can also occur as far-field boundary conditions in acoustics, electromagnetics, or fluid mechanics. Nonlocal boundary conditions are handled with integral equations, and are not supported in the current version of Sundance.It is often possible to find a local approximation to a nonlocal boundary condition, which will allow you to proceed at the prce of introducing some modeling error.


