|
STA
6166 UNIT 3 Section 2 Answers
|
| Welcome | < | Begin | < | < | Unit 3 Section 2 Answers | |||||
| To Ag and Env. Answers |
| To Tox and Health Answers |
| To Social and Education Answers |
| To Engineering Answers |
Unit 3 Section 2 Answers
Social and Education
- Using the data and analysis from the previous exercise (Unit 3 Section 1), perform a multiple comparison analysis, with experimentwise Type I error rate of 0.05, using each of the following procedures:
- Fisher's LSD
- Student-Newman-Keuls
- Tukey's W
- Duncan's MCP
- Waller-Duncan
- Using these same data, test the contrast
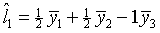 where
t=1 for age group A, t=2 for age group B, t=3 for age group C.
where
t=1 for age group A, t=2 for age group B, t=3 for age group C.
If you transformed the data prior to the analysis of variance, the multiple comparison procedures should be performed on the transformed data as well.
Only the appropriate statistics, critical values and results are given for each procedure. This analysis was run in SAS. Other packages only provide limited multiple comparison procedures. You can compare these results to those you obtained by hand calculations.
OVERVIEW
Means with the same letter are not significantly different
Level of ----------attention----------
group N Mean Std Dev LSD* TUKEY SNK DUNCAN WALLER*
A 10 22.9000000 13.1271559 A A A A A
B 10 19.6000000 10.8545945 A A A A A
C 10 21.9000000 13.3287492 A A A A A
* Technically, since the overall F-test was not significant, we would never run the
Fisher's LSD or the WALLER procedure.
t Tests (LSD)
Alpha 0.05
Error Degrees of Freedom 27
Error Mean Square 155.9333
Critical Value of t 2.05183 <- From T table.
Least Significant Difference 11.458
Tukey's Studentized Range (HSD) Test
Alpha 0.05
Error Degrees of Freedom 27
Error Mean Square 155.9333
Critical Value of Studentized Range 3.50643 <- From Table 10 (q)
Minimum Significant Difference 13.846
Student-Newman-Keuls Test
Alpha 0.05
Error Degrees of Freedom 27
Error Mean Square 155.9333
Number of Means 2 3
Critical Range 11.458488 13.846314 <- By equation using values
from Table 10 q=(2.9017, 3.506
Duncan's Multiple Range Test
Alpha 0.05
Error Degrees of Freedom 27
Error Mean Square 155.9333
Number of Means 2 3
Critical Range 11.46 12.04 <- By equation using values from Duncan's table
q'=(2.90211,3.048997)
Waller-Duncan K-ratio t Test
Kratio 100
Error Degrees of Freedom 27
Error Mean Square 155.9333
F Value 0.18 <- From AOV
Critical Value of t 2.62873 <- From Waller Table
Minimum Significant Difference 14.68
No Transformation needed.
Contrast DF Contrast SS Mean Square F Value Pr > F
l1 1 2.81666667 2.81666667 0.02 0.8941
- Let us take the output apart and see what we have.
- The contrast SS is the contrast sums of squares.
- This is the equation at the bottom of page 433 in the book.
- The mean square is the contrast SS divided by the degrees of freedom which is one, since there is only one equation in the contrast being tested.
- The F-value is the F-statistic as calculated from the equation on page 436, ie. the Contrast mean square divided by the Mean Square error from the AOV table.
- If you divide the Contast SS by the MSE you get the F-statistic. The pr > F value is the p-value associated with the observed F-value from an F table with ndf=1, ddf=error df .
- Hence everything you need to perform the requested test was here.