1. Using the data and analysis from the previous exercise (Unit 3 Section 1), perform a multiple comparison analysis, with experimentwise Type I error rate of 0.05, using each of the following procedures:
   Fisher's LSD
   Student-Newman-Keuls
   Tukey's W
   Duncan's MCP
   Waller-Duncan
2. If you transformed the data prior to the analysis of variance, the multiple comparison procedures should be performed on the transformed data as well.
3. Using these same data, test the contrast 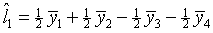where t=1 for variety A, t=2 for variety B, etc.

Answers:

Only the appropriate statistics, critical values and results are given for each procedure. This analysis was run in SAS. Other packages only provide limited multiple comparison procedures. You can compare these results to those you obtained by hand calculations.

 
OVERVIEW
Means with the same letter are not significantly different
Level of           ------------yield------------                             
variety      N             Mean          Std Dev  LSD TUKEY SNK DUNCAN WALLER
                                                                             
A            8       3.06250000       0.40333432   A    A    A    A      A   
B            8       3.72500000       0.42342144   B    B    B    B      B   
C            8       4.00000000       0.55032458   B    B    B    B      B   
D            8       2.90000000       0.39279220   A    A    A    A      A   


    t Tests (LSD) for yield (Fisher's LSD)
          Alpha                          0.05
          Error Degrees of Freedom       28
          Error Mean Square              0.199777
          Critical Value of t            2.04841
          Least Significant Difference   0.4578
   Tukey's Studentized Range (HSD) Test for yield
          Alpha                                 0.05
          Error Degrees of Freedom              28
          Error Mean Square                     0.199777
          Critical Value of Studentized Range   3.86125   <- Table 10 value
          Minimum Significant Difference        0.6102
    Student-Newman-Keuls Test for yield
          Alpha                          0.05
          Error Degrees of Freedom       28
          Error Mean Square              0.199777
          Number of Means               2           3           4
          Stud.Range Crit. Val      2.897       3.499     3.86125  <- Table 10
          Critical Range        0.4577838   0.5529593   0.6101757
   Duncan's Multiple Range Test for yield
          Alpha                          0.05
          Error Degrees of Freedom       28
          Error Mean Square              0.199777
          Number of Means          2          3          4
          Table Value           2.90       3.04       3.13   <- From Duncan Table
          Critical Range       .4578      .4810      .4960  
   Waller-Duncan K-ratio t Test for yield
          Kratio                               100
          Error Degrees of Freedom             28
          Error Mean Square                    0.199777
          F Value                              11.05       <- From AOV 
          Critical Value of t                  1.92620     <- From Waller Table
          Minimum Significant Difference       0.4305

No transformation used.

Contrast   DF     Contrast SS     Mean Square    F Value    Pr > F
l1         1       0.02531250      0.02531250       0.13    0.7245

• Let us take the output apart and see what we have.
• The contrast SS is the contrast sums of squares.
• This is the equation at the bottom of page 433 in the book.
• The mean square is the contrast SS divided by the degrees of freedom which is one, since there is only one equation in the contrast being tested.
• The F-value is the F-statistic as calculated from the equation on page 436, ie. the Contrast mean square divided by the Mean Square error from the AOV table.
• If you divide the Contast SS by the MSE you get the F-statistic. The pr > F value is the p-value associated with the observed F-value from an F table with ndf=1, ddf=error df .
• Hence everything you need to perform the requested test was here.