Unit 3 Section 2 Answers

General Questions.

How is data dredging or data snooping different from performing multiple comparison procedures?

Multiple comparison procedures are well thought-out approaches to answering the question of which treatments are statistically different from which other treatments. They have prespecified Type I error rates associated with them to assure decreased probabilities of saying a difference is significant when in fact it is simply a sampling error. Typically all possible pairwise comparisons of treatments are examined.

In data dredging or data snooping, the researcher depends too much on the data at hand and too little on sound statistical concepts. For example, suppose we collect data from a situation where the null hypothesis is true, that is, there are no differences between the means of the t treatments. Now suppose once you collect your data you rank the t treatments by their sample means. By sampling variation, these t treatment means will be different. Also because of sampling variation, each time the overall experiment were preformed, the ranking of the treatment means will change since it is only random variation that produces the ranking. Now, also suppose for the one sample you have, you rank the treatments by their sample means and proceed to only compare the treatment with the largest mean to the treatment with the smallest mean. These two means will be much farther apart than would be the means of any two independent samples from the same population simply because of sampling variation and because we choose the largest and smallest means. Because of this, you would reject the null hypothesis that the two means are equal more often than you would for any two treatments selected at random. That is the probability of rejecting the null hypothesis when the null hypothesis is true, a Type I error, would occur much more often than expected if we were just comparing the treatments with largest to smallest means. Hence the researcher engaging in this form of data snooping has a much higher chance of making a Type I error than they think. This leads to more incorrect decisions.

The equation below provides a 95% confidence interval for the difference between two population means. What is the s_p term and how is it estimated?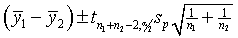

The s_p term represents the estimate of the underlying common variance for the groups. It is computed by pooling information from all the groups. For analysis of variance models, s_p is estimated as the square root of the Mean Square Error (MSE) term in the analysis of variance table.

Consider the following equations. Indicate with a check in the appropriate box which are true linear contrasts.

Equation Contrast Not Contrast

+

+

+

+

Is equation l₁ above orthogonal to l₂?

Orthogonality is determined by summing the product of the coefficients of the two contrasts in question. In this case a1b1+a2b2+a3b3 = (1)(1)+(1)(2) +(-2)(-3) = 1 + 2 -6 = -3. Because this sum is not equal to zero (0), the two contrasts are not orthogonal. [Note that none of the true contrasts above are orthogonal].

In problem 8.12, page 416, Ott and Longnecker describe a strawberry preservation study involving three preservatives and a no treatment control. This resulted in four treatment groups (t=4), denoted (Control, A, B, C). Assume the four sample means are given by 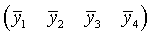respectively. For each of the following questions write a linear contrast in the four means that would be used to answer the question.

Q1: Is Treatment A different from the no-treatment Control?

Contrast coefficient vector: (1 -1 0 0) or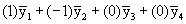

Q2: Is the average of treatments A, B and C different from the no-treatment control?

Contrast coefficient vector: (1 -1/3 -1/3 -1/3) or 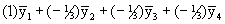; or (3 -1 -1 -1) or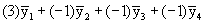

Q3: Is Treatment A different from Treatment C?

Contrast coefficient vector: (0 1 0 -1) or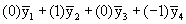

Q4: Is the average of Treatments A and B different from Treatment C?

Contrast coefficient vector: (0 1/2 1/2 -1) or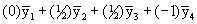

In the discussion of individual comparison Type I error rates and experimentwise Type I error rates an equation is given which describes the relationship between the two. Suppose we have t=9 treatments and we wish to look at all t(t-1)=m=72 individual contrasts. What value should we use for the individual comparison Type I error rate (a_I) to achieve an overall error rate of a_E=0.05?

The equation is given on page 439 in the book.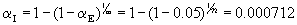

Which of the following multiple comparison procedures are most conservative (in the sense that one is least likely to make a Type I experimentwise error)?

Fisher's LSD

Student-Newman-Keuls

Tukey's W

Duncan's MCP

Waller-Duncan

Tukey's W