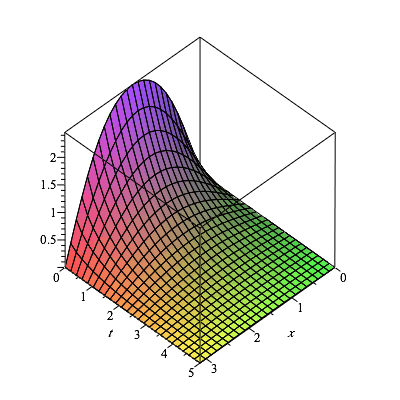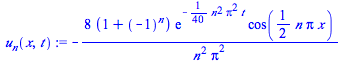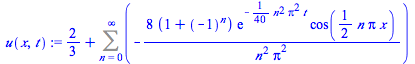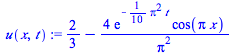m4354_heat_examples.mw
Some Examples Using Maple to Solve the Heat Equation
Example 1 Heat Equation Dirichlet Conditions
Assignment of system parameters
Eigenvalues and orthonormal eigenfunctions.
| > |
mu[n]:=(n*Pi/L); lambda[n]:=-mu[n]^2; |
for n = 1, 2, 3, ... Orthonormal eigenfunctions
| > |
X[n](x):=sqrt(2/L)*sin(n*Pi/L*x);X[m](x):=subs(n=m,X[n](x)): |
Statement of orthonormality
| > |
Int(X[n](x)*X[m](x),x=0...L)=delta(n,m); |
Time-dependent solution
| > |
T[n](t):=C(n)*exp(k*lambda[n]*t);
|
| > |
u[n](x,t):=T[n](t)*X[n](x); |
Eigenfunction expansion
| > |
u(x,t):=Sum(u[n](x,t),n=1..infinity); |
Evaluation of Fourier coefficients for the specific initial condition
| > |
C(n):=Int(f(x)*X[n](x),x=0..L);C(n):=expand(value(%)): |
| > |
C(n):=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},C(n)));
|
Check Fourier coefficients
| > |
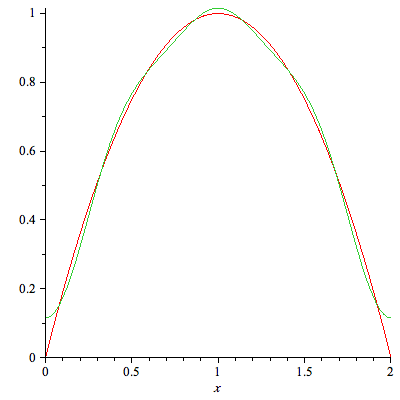
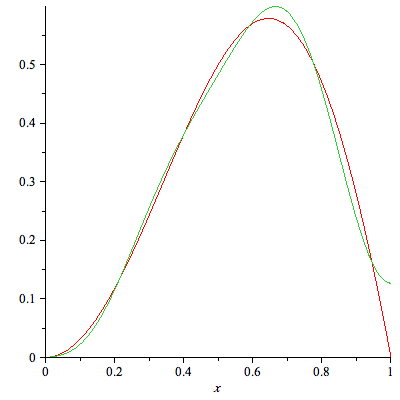
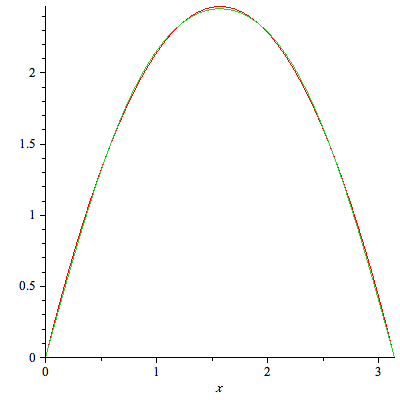
plot({f(x),sum(C(n)*X[n](x),n=1..3)},x=0..L); |
Our simple solutions
| > |
u[n](x,t):=eval(T[n](t)*X[n](x)); |
Series solution
| > |
u(x,t):=Sum(u[n](x,t),n=1..infinity); |
First few terms of sum
| > |
u(x,t):=sum(u[n](x,t),n=1..3); |
Animation
| > |
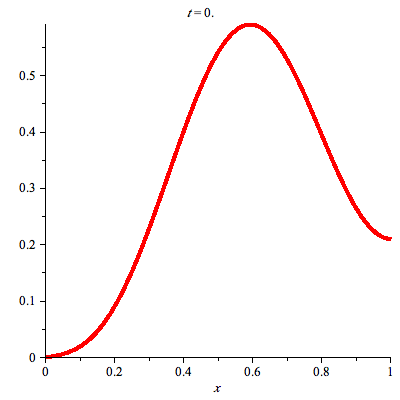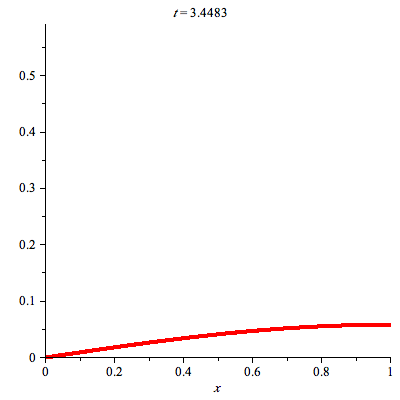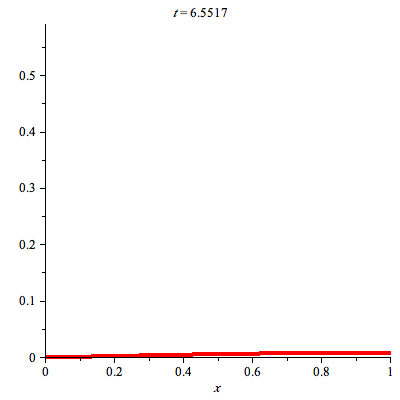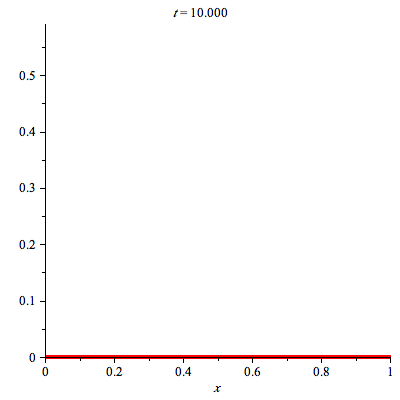
animate(plot,[u(x,t),x=0..L],t=0..10,color=red,thickness=3, numpoints=200, frames=30); |
The preceding animation command illustrates the spatial-time dependent solution for 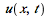 . The animation sequence shows snapshots at times
. The animation sequence shows snapshots at times 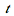 = 0, 1, 2, 3, 4, and 5.
= 0, 1, 2, 3, 4, and 5.
Animation Sequence
| > |
u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)): |
| > |
u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)): |
| > |
u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)): |
| > |
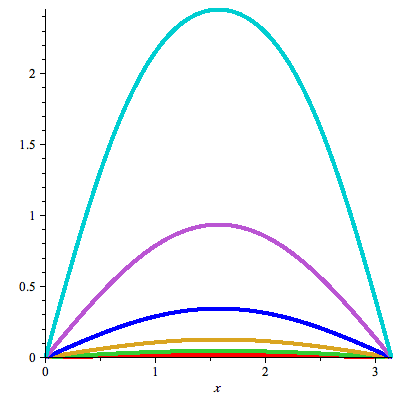
plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..L,thickness=3); |
| > |
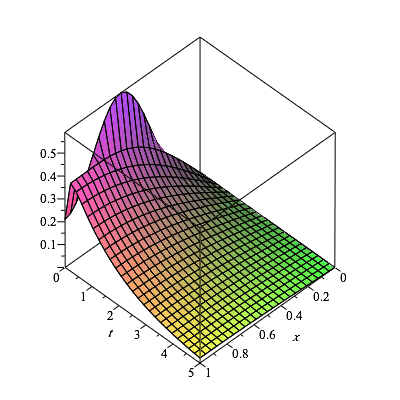
plot3d(u(x,t),x=0..L,t=0..5,axes=boxed); |
Example 2 Heat Equation Neumann Conditions
Assignment of system parameters
Eigenvalues and orthonormal eigenfunctions.
| > |
mu[n]:=(n*Pi/L); lambda[n]:=-mu[n]^2; |
for n = 1, 2, 3, ... Orthonormal eigenfunctions
| > |
X[n](x):=sqrt(2/L)*cos(n*Pi/L*x);X[m](x):=subs(n=m,X[n](x)): |
Statement of orthonormality
| > |
Int(X[n](x)*X[m](x),x=0...L)=delta(n,m); |
Time-dependent solution
| > |
T[n](t):=C(n)*exp(k*lambda[n]*t);
|
| > |
u[n](x,t):=T[n](t)*X[n](x); |
| > |
u[0](x,t):=C(0)*X[0](x); |
Eigenfunction expansion
| > |
u(x,t):=u[0](x,t)+Sum(u[n](x,t),n=1..infinity); |
Evaluation of Fourier coefficients for the specific initial condition
| > |
C(n):=Int(f(x)*X[n](x),x=0..L);C(n):=expand(value(%)): |
| > |
C(n):=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},C(n)));
|
| > |
C(0):=Int(f(x)*X[0](x),x=0..L);C(0):=expand(value(%)): |
| > |
C(0):=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},C(0))); |
Check Fourier coefficients
| > |
plot({f(x), C(0)*X[0](x)+sum(C(n)*X[n](x),n=1..7)},x=0..L); |
Our simple solutions
| > |
u[n](x,t):=eval(T[n](t)*X[n](x)); |
| > |
u[0](x,t):=C(0)*X[0](x); |
Series solution
| > |
u(x,t):=u[0](x,t)+Sum(u[n](x,t),n=0..infinity); |
First few terms of sum
| > |
u(x,t):=u[0](x,t)+sum(u[n](x,t),n=1..3); |
Animation
| > |
animate(plot,[u(x,t),x=0..L],t=0..5,color=red,thickness=3, numpoints=200, frames=30); |
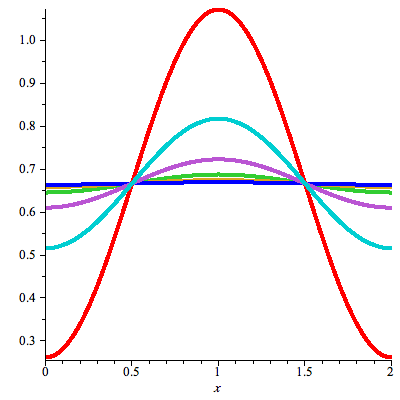
The preceding animation command illustrates the spatial-time dependent solution for 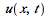 . The animation sequence shows snapshots at times
. The animation sequence shows snapshots at times 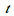 = 0, 1, 2, 3, 4, and 5.
= 0, 1, 2, 3, 4, and 5.
Animation Sequence
| > |
u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)): |
| > |
u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)): |
| > |
u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)): |
| > |
plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..L,thickness=3); |
| > |
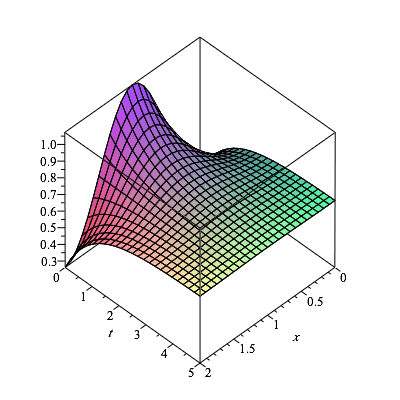
plot3d(u(x,t),x=0..L,t=0..5,axes=boxed); |
Example 3 Heat Equation Dirichlet-Neumann Conditions
Assignment of system parameters
Eigenvalues and orthonormal eigenfunctions.
| > |
mu[n]:=((2*n-1)*Pi/(2*L)); lambda[n]:=-mu[n]^2; |
for n = 1, 2, 3, ... Orthonormal eigenfunctions
| > |
X[n](x):=sqrt(2/L)*sin(mu[n]*x);X[m](x):=subs(n=m,X[n](x)): |
Statement of orthonormality
| > |
Int(X[n](x)*X[m](x),x=0...L)=delta(n,m); |
| > |
radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},int(X[n](x)^2,x=0..L))); |
Time-dependent solution
| > |
T[n](t):=C(n)*exp(k*lambda[n]*t);
|
| > |
u[n](x,t):=T[n](t)*X[n](x); |
Eigenfunction expansion
| > |
u(x,t):=Sum(u[n](x,t),n=1..infinity); |
Evaluation of Fourier coefficients for the specific initial condition
| > |
C(n):=Int(f(x)*X[n](x),x=0..L);C(n):=expand(value(%)): |
| > |
C(n):=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(-1)^n},C(n)));
|
Check Fourier coefficients
| > |
plot({f(x),sum(C(n)*X[n](x),n=1..5)},x=0..L); |
Our simple solutions
| > |
u[n](x,t):=eval(T[n](t)*X[n](x)); |
Series solution
| > |
u(x,t):=Sum(u[n](x,t),n=1..infinity); |
First few terms of sum
| > |
u(x,t):=sum(u[n](x,t),n=1..3); |
Animation
| > |
animate(plot,[u(x,t),x=0..L],t=0..10,color=red,thickness=3, numpoints=200, frames=30); |
The preceding animation command illustrates the spatial-time dependent solution for 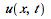 . The animation sequence shows snapshots at times
. The animation sequence shows snapshots at times 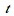 = 0, 1, 2, 3, 4, and 5.
= 0, 1, 2, 3, 4, and 5.
Animation Sequence
| > |
u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)): |
| > |
u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)): |
| > |
u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)): |
| > |
plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..L,thickness=3); |
| > |
plot3d(u(x,t),x=0..L,t=0..5,axes=boxed); |
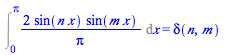
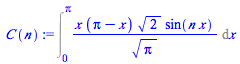

![]() . The animation sequence shows snapshots at times
. The animation sequence shows snapshots at times ![]() = 0, 1, 2, 3, 4, and 5.
= 0, 1, 2, 3, 4, and 5.