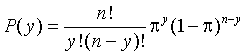You can choose to work some or all of the problems listed below. We recommend
that you at least work the problems listed in your major area of interest.
Answers to these exercises can be found here.
(ANSWERS).
| General Questions. |
- The Binomial distribution has the form:
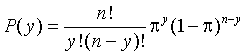
Using this equation, compute the following probabilities.
- P(y=3) given n=20 and p=.5
- P(y<4) given n=10 and p=.75
- P(y>1) given n=5 and p=.1
- Under what conditions can the formula
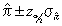 be
used to express a confidence interval for p. be
used to express a confidence interval for p.
- Using the equations on page 472-473 for the confidence interval
for a proportion, compute 95% confidence intervals for p
for the following:
- y=5, n=20 (that is, five successes in 20 trials)
- y=1, n=10
- y=0, n=75
- y=35, n=35
- Microsoft Corporation released its Windows XP operating system in
November of 2001. You have been asked to design a survey to determine
how many Windows 2000 users have already switched to Windows XP. Microsoft,
being optimistic, suspects the proportion is as high as 20%. You want
to be certain of the estimated proportion to within ±0.02 (i.e.
±2%). Determine the sample size needed for this survey using
0.2 as the guess for p. Redo the sample
size determination using 0.5 (a worst case scenario for p).
[equation on page 474].
- The sensitivity, specificity and predictive power of a diagnostic
test for a disease are defined as follows:
- Sensitivity is the probability
that the test will give a positive result (indicating the presence
of the disease) in a subject who has the disease.
- Specificity is the probability
that the test will give a negative result (indicating the absence
of the disease) in a subject who does not have the disease.
- Predictive power is the probability
that the test will make the correct diagnosis.
Back in Exercise 4.28 we were presented with a table describing the
results of a radiological determination test for presence of Appendicitis.
Suppose this study had been redone with 220 patients suspected of
having appendicitis being subjected to the radiological determination
test (CAT scan-the experimental approach) as well as to a clinical
assessment (the expensive but definitive answer). Only two posible
choices are available for each method, a decision of definitely apendicitis
(DA) or definitely not appendicitis (DNA). The result of this study
is in the table below.
| |
Clinical Assessment |
| Radiologic Determination |
Confirmed (DA) |
Ruled Out (DNA) |
| Definitely Appendicitis (DA) |
120
|
7
|
| Def. Not Appendicitis (DNA) |
10
|
83
|
| Total |
130
|
90
|
Using these data do the following:
- Estimate the sensitivity, specificity and predictive power of
the diagnostic test.
- Construct 95% confidence intervals for the parameters estimated
in (a) and interpret them.
- Perform a hypothesis test to verify the claim that the radiologic
determination will detect more than 85% of the cases who have the
disease.
- Construct a 95% lower confidence bound to the predictive power
of the test and interpret it.
|
 For
students in agriculture and environmental fields. For
students in agriculture and environmental fields. |
1. An experiment is run to examine two different methods methods of
preserving onions. The researcher proposes to compare Method A to Method
B, by storing a large number of onions using each method and after 6
months to classifying each onion as 'good' or 'defective'. The result
of the experiment is as below:
|
Experiment Result
|
Method A
|
Method B
|
|
Good
|
134
|
207
|
|
Defective
|
16
|
33
|
|
Total number
|
150
|
240
|
a. Use these data to test whether the proportion of GOOD onions in
each method are different from each other. Use a=.05.
b. Calculate a 95% confidence interval for the difference tested above.
2. A second aspect of the study was to examine the effects of different
fertilizer treatments on the incidence of blackleg (Bacterium phytotherum)
on potato seedlings. Seedlings were randomly assigned to a fertilizer
treatment and after three weeks classified as to whether it was contaminated
by blackleg or free. The results for four treatment were as follows:
| Observed frequencies |
Blackleg |
Total |
| 1.No fertilizer |
16 |
101 |
| 2.Nitrogen only |
10 |
95 |
| 3.Dung
only |
4 |
113 |
| 4.Nitrogen
and dung |
14 |
141 |
Use these data to determine if the presence of Blackleg is independent
of the Fertilization method. Use a=.05.
|
 For
students in engineering fields. For
students in engineering fields. |
1. A project manager for an engineering firm submitts a bid for engineering
design for two projects. The firm formally evaluates the chances that
each bid will be accepted by surveying its engineers. The following
table summarizes the collective assessment from this survey.
| Results of bids |
Project A
|
Project B
|
| Accepted |
28
|
25
|
| Refused |
29
|
24
|
| Total number of bits submitted |
57
|
49
|
a. Test whether the chances that each bid was accepted
are different. Use a=.05.
b. Calculate a 95% confidence interval for the difference
of chances that each bid was accepted.
2. An study plans to assess the impact
of several factors involving the heat treatment of leaf springs. In
this process, a conveyor system transports leaf spring assemblies through
a high-temperature furnace. After heating, a high-pressure press induces
curvature in the medal. Once the spring leaves the press, an oil quench
cools it to near ambient temperature. An important quality characteristic
of this process is the resulting free height of the spring. The researchers
are interested in examining four factors known to affect this free height.
For each spring tested, the final classification is whether the spring
is below the specified minimal spring height. Results of numerous tests
are given in the following table.
|
Factors
|
Low level
|
Total
|
|
1.High heat temp.
|
14
|
32
|
|
2.heating
time
|
23
|
48
|
|
3.Transfer
time
|
10
|
22
|
|
4.Hold
down time
|
2
|
5
|
Use these data
to run a Chi-square test to determine whether a finding of low level
is independent of the factors used. Use a=.05.
|
 For
students in toxicology and health science fields. For
students in toxicology and health science fields. |
1. In a study of children aged 0 to15, concern is focused on the presence
or absence of the carrier for Streptococcus Pyogenesis
and the relationship between the presence of the carrier and tonsil
size.
| |
Tonsils present. Not enlarged
|
Tonsils enlarged
|
| Presence of the carrier |
15
|
19
|
| Absence of the carrier |
380
|
360
|
| Total number |
395
|
379
|
a. Is the presence of the carrier related to whether tonsils
are enlarged or not. Test this hypothesis at the P(Type I error)=a=.05
level.
b. Calculate a 95% confidence interval for
the difference between the Tonsils enlarged probabilities in the presence
of the carrier versus that in the absence of the carrier.
2. In a controlled clinical trial to determine the efficiency
of an experimental drug for treating migraine headache, patients were
divided into four groups and were treated with four drugs: A, B, C and
D. Each treatment lasted 12 weeks. At the end of the treatment period,
the effect of the drug was classified into two categories:
effective and not effective. The migraine headache data obtained
are as follows:
|
Drug
|
Effective
|
Total
|
|
A
|
26
|
45
|
|
B
|
14
|
28
|
|
C
|
10
|
17
|
|
D
|
22
|
90
|
Use these data to run a chi-square test to determine whether the effectiveness
of all drugs are the same.This is equivalent to testing that all effectiveness
proportions are the same.
|
 For
students in community development, education and social services fields. For
students in community development, education and social services fields. |
1. A company uses a pre-employment test to screen applicants
for sales jobs. We are interested in whether the screning test is effective.
In an experiment, a random samples of applicants
who pass the test and a second sample of those who do not pass the screening
test are all employed. The number of employees who successfully completed
the training program in these two samples was recorded as follows.
| Experiment Result |
Applicant who pass the pre-employment
test
|
Applicant who do not pass the pre-employment
test
|
| Employees completed in the training
program |
67
|
15
|
| Employees failed in the training
program |
28
|
22
|
| Total number of Employees |
95
|
37
|
a. Test whether the proportions of employee who successfully completed
the training program is the same for the group who initially passed
the pre-employment test to those who did not initially pass the pre-emplyment
test. For this test use P(Type I error)=a=.05.
b. Calculate a 95% confidence interval for the
above difference.
2.A survey was made of 164 customers
in a department store. These customers were divided into four groups
with members of each group viewing only one of the four types of advertisements
available for a certain product. The total numbers of customers who
made purchases by viewing group are given below.
|
Four
types of advertisement
|
Customers
made purchases
|
Total
|
|
1.Advertisement
A
|
27
|
39
|
|
2.Advertisement
B
|
29
|
51
|
|
3.Advertisement
C
|
17
|
31
|
|
4
Advertisement D
|
9
|
23
|
Can we determine from this whether there is a difference in the purchase
fraction across the four groups? |