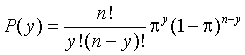
STA 6166 UNIT 3 Section 3 Exercises
Welcome < Begin <

Section 3

 < Unit 3 Section 3 Answers
To Ag and Env. Answers
To Tox and Health Answers
To Social and Education Answers
To Engineering Answers

 

Unit 3 Section 3 Answers

General Questions

1. The Binomial distribution has the form:
Using this equation, compute the following probabilities.
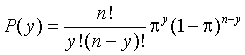
    P(y=3) given n=20 and p=.5 ==> 0.001087189
    P(y<4) given n=10 and p=.75 ==> 0.003505707 [ remember 4 not included]

    P(y>1) given n=5 and p=.1 ==> 0.08146 [ compute 1-p(y=0)-p(y=1) ]

    I used EXCEL to make this computations. The equation is as follows

    P(Y=y)=((FACT(B2)/(FACT(A2)*FACT(B2-A2)))*(C2^A2)*((1-C2)^(B2-A2)))

    with n in B, y in A, p in C.

2. Under what conditions can the formula be used to express a confidence interval for p.

Page 472 in the Book "The normal approximation to the distribution of can be applied unde the same conditions as that for approximating by using a normal distribution." What this says is that the sample proportion is nothing more than a sample mean. The central limit theorem works for the sample proportion in exactly the same way it works for the sample mean. Note also on page 473 it says: "The confidence interval for p is based on a norma approximation to a binomial, which is appropriate provided n is sufficiently large. The rule we have specified is that both np and n(1-p) should be at least 5, but since p is the unknown parameter, we'll require that nand n(1- ) be at least 5. " Thus, the normal approximation really only begin to kick in once this latter condition is satisfied. Remember also that this is a minimal condition, more is better here.

3. Using the equations on page 472-473 for the confidence interval for a proportion, compute 95% confidence intervals for p for the following:

For the first two, we use the equations on page 472.

For the first set we have: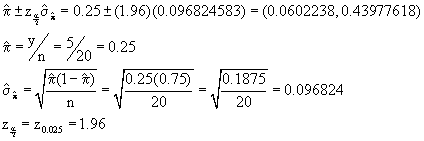

When our estimate of p is 0 or 1, the equations above produce a standard error that is zero. Note that on page 473 there is an alternative estimate for the sample proportion and associated standard error and confidence interval when y=0 or when y=n.

4. Microsoft Corporation released its Windows XP operating system in November of 2001. You have been asked to design a survey to determine how many Windows 2000 users have already switched to Windows XP. Microsoft, being optimistic, suspects the proportion is as high as 20%. You want to be certain of the estimated proportion to within ±0.02 (i.e. ±2%). Determine the sample size needed for this survey using 0.2 as the guess for p. Redo the sample size determination using 0.5 (a worst case scenario for p). [equation on page 474].

Set p=0.2 (our optimistic estimate), and E=0.02 (the ±2% target precision), then our estimated sample size is: 1536.64 or rounded up to 1537.

For the worst case scenario, set p=0.5 and redo the above computations. Here n= 2401 (or exactly 864 or 56% more subjects). Note that as the proportion goes down or up from 0.5, the needed sample size goes down as well.

p 0.2 0.3 0.4 0.5 0.60 0.7 0.8
n 1537 2017 2305 2401 2305 2017 1537

5. The sensitivity, specificity and predictive power of a diagnostic test for a disease are defined as follows:

  1. Sensitivity is the probability that the test will give a positive result (indicating the presence of the disease) in a subject who has the disease.
  2. Specificity is the probability that the test will give a negative result (indicating the absence of the disease) in a subject who does not have the disease.
  3. Predictive power is the probability that the test will make the correct diagnosis.
Back in Exercise 4.28 we were presented with a table describing the results of a radiological determination test for presence of Appendicitis. Suppose this study had been redone with 220 patients suspected of having appendicitis being subjected to the radiological determination test (CAT scan-the experimental approach) as well as to a clinical assessment (the expensive but definitive answer). Only two posible choices are available for each method, a decision of definitely apendicitis (DA) or definitely not appendicitis (DNA). The result of this study is in the table below.
      Clinical Assessment
    Radiologic Determination Confirmed (DA) Ruled Out (DNA)
    Definitely Appendicitis (DA)
    120
    7
    Def. Not Appendicitis (DNA)
    10
    83
    Total
    130
    90
Using these data do the following:

Estimate the sensitivity, specificity and predictive power of the diagnostic test.

Sensitivity = (Radiologic DA) / (Clinical DA) = 120/130 = 0.9230769

Specificity = 83/90 = (Radiologic DNA) / (Clinical DNA) = 0.92222222

Predictive power = (Correct Answer)/(All tested) = (120 + 83) / (130 + 90) = 0.9227273

Construct 95% confidence intervals for the parameters estimated in (a) and interpret them.

95% CI for Sensitivity = (0.877269942, 0.968883904) Based on the sample size and taking into account sampling variability, the true value of sensitivity for the radiological test could be as low as 87.7% or as high as 96.9% with 95% confidence. In repeated executions of this same sized experiment, a confidence interval constructed as described above would contain the true sensitivity value 95% of the time.

95% CI for Specificity = (0.866889712, 0.977554733) "same interpretation as above"

95% CI for Predictive Power = (0.887441915, 0.958012631) "same interpretation as above"

Perform a hypothesis test to verify the claim that the radiologic determination will detect more than 85% of the cases who have the disease.

This test addresses a hypothesis that the True sensitivity of the test is 0.85. You are not give an alternative, hence we might test a one-sided hypothesis that the sensitivity is greater than 0.85 (i.e. is actually better than expected) or a two sided test that the true sensitivity is not equal to 0.85 (i.e. is actually different than expected).

H0: psensitivity = 0.85

HA1: psensitivity > 0.85

HA2: psensitivity not equal to 0.85


T.S.

R.R. (One Sided) Reject if z > za = 1.645 (Two Sided) Reject if z > za/2 = 1.96

Conclusion: Since the value of the test statistic is greater than the critical value for either the one-sided test or the two-sided test, we conclude that not only is the sensitivity not equal to 0.85, but that it is significantly greater than 0.85.

 

Construct a 95% lower confidence bound to the predictive power of the test and interpret it.

You might think that we have performed this task above. I.e, the 95% lower confidence bound to the predictive power is 0.8874. Thus, in normal discussion you would say that you are 95% confident that the true predictive power of the test is greater than 0.8874.

But wait, let us think about this. When we construct the 95% confidence interval we say that "in repetitions of this same sized study, in 95% of the repetitions, a confidence interval constructed in this way would contain the true population proportion." Likewise, in 5% of the repetitions the confidence interval would not contain the true proportion. What does this say about the lower bound of the CI? Well, in the 5% of cases where we make an error, we expect half of these mistakes to be outside the bound on the high side and half to be outside on the low side (kind of extending the symmetry of the Normal distribution assumed under the central limit theorem). Hence we would expect only a 2.5% chance that the true mean would be below the 0.8874 estimate. This tells me that I should compute a 90% confidence interval and use its lower bound to answer the above question. In that case, I would be confident that in 5% of cases the true proportion is below the lower bound estimate and in 95% of cases it is above the estimate.

The 90% CI for predictive power is (0.893112776, 0.95234177). Hence I would be 95% confident that the true predictive power of the test is at least 89.3%.