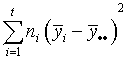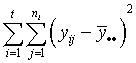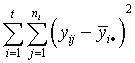You can choose to work some or all of the problems listed below. We recommend
that you at least work the problems listed in your major area of interest.
Answers to these exercises can be found here (ANSWERS).
| General Questions. |
- In this section we discuss comparing means from a number of populations.
Can you think of a situation where one might wish to compare variances
among populations? compare upper quartiles among populations?
- List the three assumptions under which analysis of variance procedures
are developed (see page 385).
- The sample variance of the means of the multiple populations is
given as
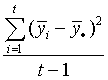 . Is
this the within means variance SW2 or the between
means variance, SB2? . Is
this the within means variance SW2 or the between
means variance, SB2?
- The F-test for equality of means from multiple populations if formed
from the ratio of two variance estimates. Which of the test statistics
below is the correct ratio?
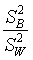 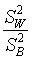
- One column of the analysis of variance table for a completely randomized
design consists of some sums of squares. Below are two column lists.
In the first column are the names of the sums of squares and in the
second column are the equations for the sums of squares. Match the
equations with their correct names.
| TSS (total sums of squares) |
a. 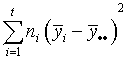 |
| SSW (within sample sums of squares) |
b. 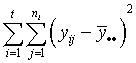 |
| SSB (between sample sums of squares) |
c. 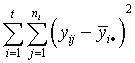 |
- Suppose you have performed an experiment using a completely randomized
design to compare t=5 treatments. Each treatment has been replicated
ni=4 times. Complete the table below with the appropriate degrees
of freedom.
| Source |
Degrees of Freedom |
| Between samples |
|
| Within samples |
|
| Totals |
|
- Using the degrees of freedom from the table above and Table 8 in
the book, what is the critical value for the F test at a type I error
rate of 5%?
- The linear model typically used to analyze a one-way classification
study (completely randomized design) has the form:
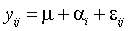 .
Describe in your own words what each term of the model describes about
the data. For example, the m term describes
the overall average for the data. .
Describe in your own words what each term of the model describes about
the data. For example, the m term describes
the overall average for the data.
- Can you explain why the null hypothesis that all the ai
terms are equal to zero is equivalent to the hypothesis that all treatment
means are the same.
- Below are listed typical responses that would not be expected to
have homogeneous variances. Beside each response list the transformation
typically used prior to the analysis of variance in an attempt to
produce more homogeneous variances.
| Response |
Transformation
|
| Counts between 0 and 10 |
|
| Counts above 10 |
|
| Proportion |
|
| Percentage |
|
| Rate |
|
- How does the hypothesis of the Kruskal-Wallis Test differ from the
hypothesis tested with the usual analysis of variance procedures?
|
 For
students in agriculture and environmental fields. For
students in agriculture and environmental fields. |
Problem 8.17 in Ott and Longnecker. Researchers record the yields of
corn, in bushels per plot, for four different varieties of corn, A,
B, C, and D. In a controlled greenhouse experiment, the researchers
randomly assign each variety to eight of 32 plots available for the
study. The yields are listed here.
A B C D
2.5 3.6 4.3 2.8
3.6 3.9 4.4 2.9
2.8 4.1 4.5 3.1
2.7 4.3 4.1 2.4
3.1 2.9 3.5 3.2
3.4 3.5 3.4 2.5
2.9 3.8 3.2 3.6
3.5 3.7 4.6 2.7
- Write the linear model for these data.
- Perform a one-way analysis of variance. Test the hypothesis of no
differences in average yields at a type I error rate of 5%.
- Test the hypothesis of equal variances. Do these data need to be
transformed? If so, what transformation would you use?
- For each variety, compute the sample mean and subtract this mean
from each observation (i.e. center each variety). Combine all these
"residuals" into on data set and test for normality. Is
there any indication that these data are not normal.
- Perform the Kruskal-Wallis test on these data. How do the results
compare to the analysis of variance procedure?
|
 For
students in engineering fields. For
students in engineering fields. |
Problem 8.30, page 424 of Ott and Longnecker. A small corporation make
insulation shields for electrical wires using three different types
of machines. The corporation wants to evaluate the variation in the
inside diameter dimension of the shields produced by the machines. A
quality engineer at the corporation randomly selects shields produced
by each of the machines and records the inside diameters of each shield
(in millimeters). She wants to determine whether the means and standard
deviations of the three machines differ. The data are given below.
Machine_C Machine_B Machine_A
29.7 8.7 18.1
18.7 56.8 2.4
16.5 4.4 2.7
63.7 8.3 7.5
18.9 5.8 11.0
107.2 . .
19.7 . .
93.4 . .
21.6 . .
17.8 . .
- Write the linear model for these data.
- Perform a one-way analysis of variance. Test the hypothesis of no
differences in average shield diameters at a type I error rate of
5%.
- Test the hypothesis of equal variances. Do these data need to be
transformed? If so, what transformation would you use?
- For each machine, compute the sample mean and subtract this mean
from each observation (i.e. center each machine's data). Combine all
these "residuals" into on data set and test for normality.
Is there any indication that these data are not normal.
- Perform the Kruskal-Wallis test on these data. How do the results
compare to the analysis of variance procedure?
|
 For
students in toxicology and health science fields. For
students in toxicology and health science fields. |
From problem 9.24,page 464 in Ott and Longnecker. Researchers conducted
a study of the effects of three heartworm drugs on the fat content of
the shoulder muscles in Labrador retrievers. Twenty (20) dogs were randomly
divided into four treatment groups of five (5) dogs each. Dogs in group
A were assigned to the untreated control. The remaining three groups
identify which of the heartworm drug all dogs in the group received.
At the end of two years of treatment, the percentage fat content of
the shoulder muscles was determined and is given here.
A B C D
2.64 3.24 2.90 2.91
2.56 3.71 3.02 2.89
3.30 2.95 3.78 3.21
2.19 3.01 2.96 2.89
2.45 3.08 2.87 2.68
- Write the linear model for these data.
- Perform a one-way analysis of variance. Test the hypothesis of no
differences in average fat content at a type I error rate of 5%.
- Test the hypothesis of equal variances. Do these data need to be
transformed? If so, what transformation would you use?
- For each group, compute the sample mean and subtract this mean from
each observation (i.e. center each group's data). Combine all these
"residuals" into on data set and test for normality. Is
there any indication that these data are not normal.
- Perform the Kruskal-Wallis test on these data. How do the results
compare to the analysis of variance procedure?
|
 For
students in community development, education and social services fields. For
students in community development, education and social services fields. |
A large advertising firm specializes in creating television commercials
for children's products. A study is designed to test whether there are
large differences in attention span for children in three different
age groups (Group A 5-6 years, Group B 7-8 years, Group C 9-10 years).
Ten children for each group are selected at random from a large population
of children and asked to watch a 60-second breakfast cereal commercial.
Researchers record their attention span during the viewing of the commercial.
Times (in seconds) are given below.
A B C
19 19 37
36 35 6
40 22 28
30 28 4
4 1 32
10 27 16
30 27 8
5 16 41
34 3 29
21 18 18
- Write the linear model for these data.
- Perform a one-way analysis of variance. Test the hypothesis of no
differences in average attention time at a type I error rate of 5%.
- Test the hypothesis of equal variances. Do these data need to be
transformed? If so, what transformation would you use?
- For each group, compute the sample mean and subtract this mean from
each observation (i.e. center each group's data). Combine all these
"residuals" into on data set and test for normality. Is
there any indication that these data are not normal.
- Perform the Kruskal-Wallis test on these data. How do the results
compare to the analysis of variance procedure.
|
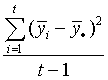 . Is
this the within means variance SW2 or the between
means variance, SB2?
. Is
this the within means variance SW2 or the between
means variance, SB2?