The sample variance of the means of the multiple populations is given as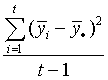 .
Is this the within means variance SW2 or the between
means variance, SB2?
.
Is this the within means variance SW2 or the between
means variance, SB2?
MSB = SB2
|
STA
6166 UNIT 3 Section 1 Answers
|
| Welcome | < | Begin | < | < | Unit 3 Section 1 Answers | > | Section 2 | |||||
| To Ag and Env. Answers |
| To Tox and Health Answers |
| To Social and Education Answers |
| To Engineering Answers |
1. In this section we discuss comparing means from a number of populations. Can you think of a situation where one might wish to compare variances among populations? compare upper quartiles among populations?
Example: (Variability)You are responsible for a machine that produces plate glass. For vision purposes, changes in the thickness of the glass from batch to batch is not that critical, but variability of the thickness of the glass within a batch, especially in a quarter square meter area might be very important.
Example: (Variability) You are planning to grow flowers (say lilies) for the general public. While the average height of the flower above its pot is not that important, wide variability in flower heights from pot to pot may be seen as a detrimental visual characteristic. The buyer, when viewing the flowers in the greenhouse may be quite interested in a consistent height plant.
Example: (Upper Quartile) Any product that has to fit into a specified space would be a good candidate for an upper quartile comparison. Two machines make bolts that attach the cylinder head to the main block of an automotive engine. The holes are predrilled and tapped so the bolts must fit. The bolt can be a little small for the hole and it will still work, but a bolt that is too large for the hole simply will not work and will be considered a lost product. We might compare the two machines on their ability to produce fewer numbers of "too large" bolts.
List the three assumptions under which analysis of variance procedures are developed (see page 385).
The sample variance of the means of the multiple populations is given as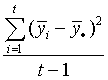 .
Is this the within means variance SW2 or the between
means variance, SB2?
.
Is this the within means variance SW2 or the between
means variance, SB2?
MSB = SB2
Correct
Wrong
One column of the analysis of variance table for a completely randomized design consists of some sums of squares. Below are two column lists. In the first column are the names of the sums of squares and in the second column are the equations for the sums of squares. Match the equations with their correct names.
The names have been moved around to match the equations.
| SSB (between sample sums of squares) | a. 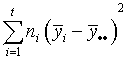 |
| TSS (total sums of squares) | b. 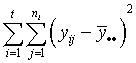 |
| SSW (within sample sums of squares) | c. 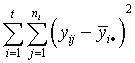 |
| Source | Degrees of Freedom |
| Between samples | t-1 = 4 |
| Within samples | 19-4 = 15 |
| Totals | (5)(4)-1 -19 |
Using the degrees of freedom from the table above and Table 8 in the book, what is the critical value for the F test at a type I error rate of 5%?
F(0.05,4,15) = 3.06
The linear model typically used to analyze a one-way classification study
(completely randomized design) has the form: ![]() .
Describe in your own words what each term of the model describes about the
data. For example, the m term describes the overall
average for the data.
.
Describe in your own words what each term of the model describes about the
data. For example, the m term describes the overall
average for the data.
Can you explain why the null hypothesis that all the ai terms are equal to zero is equivalent to the hypothesis that all treatment means are the same.
Think of it this way, the average response for the i-th group is m + ai. If all the ai are equal to zero, then the mean of each group is the same, m.
| Response |
Transformation
|
| Counts between 0 and 10 | Square Root |
| Counts above 10 | Natural Logarithm |
| Proportion | Arcsine square root |
| Percentage | Arcsine square root of percentage divided by 100. |
| Rate | Inverse or sometimes Natural Logarithm |
The Kruskal-Wallis test is a non-parametric test and as such states its null hypothesis about the equality of treatment group MEDIANS. The standard analysis of variance states it null hypothesis about the equality of treatment group MEANS (or AVERAGES).