Discrete Spaces and Functions
DiscreteFunction objects represent functions that have been discretized onto a finite element space. A finite element space is represented with a DiscreteSpace object. DiscreteFunctions are used to represent initial guesses for nonlinear and optimization problems, initial values for transient problems, and solutions of problems. To make a DiscreteFunction directly at the user level, one first creates a DiscreteSpace object.This page discusses the following topics:
- To do much of anything with discrete functions, one must understand Creation of DiscreteSpace objects.
- Once a DiscreteSpace exists, there are a number of methods of Creation of DiscreteFunctions, including Projection of expressions onto discrete spaces, Reading of discrete functions from files, and Direct creation of discrete functions.
- The vector underlying a DiscreteFunction object can be accessed either read-only or read/write. This is sometimes needed when writing interfaces to iterative algorithms such as nonlinear solvers and optimizers.
Creation of DiscreteSpace objects
A finite element space is specified by a mesh and by a basis function for each field variable to be represented. Thus a DiscreteSpace consists of a Mesh and a BasisFamily, where the BasisFamily is possibly a vector of bases.
// create a discrete space for a scalar field // with Lagrange order 1 basis functions. The vector type is not specified // so the default will be used. DiscreteSpace discSpace(mesh, new Lagrange(1));
// create a discrete space for a 3-component vector field where each component // is represented with Lagrange order 2 basis functions. The vector // type is specified through the vecType argument. DiscreteSpace discSpace(mesh, List(new Lagrange(2), new Lagrange(2), new Lagrange(2)), vecType);
Creation of DiscreteFunctions
There are several ways to create DiscreteFunctions. The starting point is always the creation of a DiscreteSpace, which is used to configure the vector underlying the discrete function. What remains is to initialize the values of this vector. The most commonly used initialization methods are Projection of expressions onto discrete spaces and Initialization to a constant value.Projection of expressions onto discrete spaces
A simple way to render an expression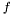 onto a discrete space
onto a discrete space 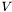 is to do an
is to do an 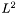 projection, in other words, to find the discrete function
projection, in other words, to find the discrete function 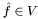 that is closest to
that is closest to 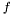 in the
in the 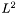 norm. This minimization problem can be set up easily in user-level Sundance using a LinearProblem, but because of its frequent occurrance we have encapsulated this capability into a specialized object called an L2Projector.
norm. This minimization problem can be set up easily in user-level Sundance using a LinearProblem, but because of its frequent occurrance we have encapsulated this capability into a specialized object called an L2Projector.An L2Projector is constructed by specifying a DiscreteSpace and an Expr to be projected onto that space:
// Set up projection on f onto the space of first-order Lagrange basis // functions on our mesh. DiscreteSpace discSpace(mesh, new Lagrange(1)); L2Projector projector(discSpace, f);
project() method, // Do the projections
Expr discreteF = projector.project();
There is a certain amount of bookkeeping involved in projection; basically, the overhead required for the setup of the linear problem doing the projection. If you need to do many projections of the same expression (perhaps with changing values of a discrete field or parameter) onto the same space, it is recommended that you create a single L2Projector and reuse it for all of these projections.
Reading of discrete functions from files
Needs to be written.Direct creation of discrete functions
With these methods we explicitly set the values of the vector underlying the discrete function. There are two direct creation methods, Initialization to a constant value and Initialization to a vector.Initialization to a constant value
One can initialize a discrete function to a constant value using one of the DiscreteFunction constructors,// Initialize a DiscreteFunction to a constant value 1.2345 DiscreteSpace discSpace(mesh, new Lagrange(1)); Expr f = new DiscreteFunction(discSpace, 1.2345);
Initialization to a vector
A DiscreteFunction can be initialized to a Trilinos Vector<double> object. It is the responsibility of the caller to ensure that the input vector is compatible with the Trilinos vector space underlying the DiscreteSpace. It is the responsibility of the caller to ensure that the ordering of vector elements is consistent with that of the DiscreteSpace. Note: This method of creation should not normally be used in top-level simulation code; it is primarily for use in writing the internals of objects such as LinearProblem.Normally, insertion of a vector into a DiscreteFunction should be done using the vector access methods described in Access to DiscreteFunction vectors
Access to DiscreteFunction vectors
Under the hood of every DiscreteFunction is a Trilinos Vector<double>. In most user-level simulation code, you will never need to use this vector explicitly. However, when writing adapters to new kinds of solvers it is sometimes necessary to modify a discrete function's vector directly.
A DiscreteFunction will normally be wrapped in an Expr object, so the first step towards vector access is to extract a DiscreteFunction pointer from an Expr. This can be done with the static method discFunc(), which has both const and non-const versions:
// Get a read-only pointer to the discrete function inside the Expr handle f0 const DiscreteFunction* discF0 = DiscreteFunction::discFunc(f0);
// Get a writable pointer to the discrete function inside the Expr handle f0
DiscreteFunction* discF0 = DiscreteFunction::discFunc(f0);
getVector() method. The discrete function can also be given a new vector by means of the setVector() method.Note: Because Expr has shallow copy behavior, changing the vector of a discrete function will simultaneously change the vector of all copies of that expression. This is a deliberate design feature: it is thereby possible to update the value of a discrete function appearing multiple times inside a complicated expression simply by setting the vector of a single instance of that discrete function.


