You can choose to work some or all of the problems listed below. We recommend
that you at least work the problems listed in your major area of interest.
Answers to this exercise can be found here.(ANSWERS)
| General Questions. |
- What is the analysis objective in regression?
- What are the steps in performing a regression analysis?
- Write out the functional form for a linear regression model?
- What is the difference between a proportional relationship and a
linear relationship?
- The error term in a linear regression model symbolically represents
two types of errors, what are they?
- How would you decide what form the relationship among your variables
should take? What are least squares parameter estimates?
- When we talk about partitioning sums of square, what are we talking
about?
- What are the two assumptions we make regarding model errors which
allow us to perform inferences on model parameters and predictions?
- When we test for a significant regression, we compare two competing
models, what are they?
- Plot a configuration of residuals which would indicate an inadequate
regression.
- If I found a standardized residual which had value -4.1, what might
I conclude?
- What characteristic must my data have if I am to attempt to compute
a pure error term?
- What does r measure?
- What does r2 measure?
- State the formal assumptions of regression analysis.
- In the prediction equation,
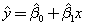 ,
what are the ,
what are the 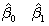 terms. terms.
|
 For
students in agriculture and environmental fields. For
students in agriculture and environmental fields. |
Air with varying concentrations of CO2 is passed over wheat
leaves at a temperature of 35°C and uptake of CO2 by the
leaves is measured. Three replications are choosen at each of four levels
of CO2 . Uptake values (y) for different concentrations (x)
are obtained and are as follows:
Concentration(x) Uptake(y)
75 .30
75 .11
75 .46
100 .65
100 .53
100 .71
125 .89
125 .81
125 1.02
150 1.20
150 1.81
150 .97
- Plot the sample data in a scatter diagram. By eye, add in the line
you think would fit the data best.
- Estimate the parameters in the model
 and then draw the fitted line onto your scatterplot.
and then draw the fitted line onto your scatterplot.
- Calculate the Analysis of Variance table and test the null hypotheses
of no significant regression. Use
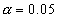
- Calculate the value of the t statistic for testing
 .
Use .
Use 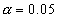 .
Show that .
Show that 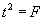 . .
- Calculate the sum of squares due to pure experimental error and
lack of fit and write the associated ANOVA table. Conduct a test for
lack of fit of the linear regression model. Does the linear regression
model fit the data well.
- Calculate the variance of both
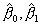 and compute the associated 95% confidence intervals.
and compute the associated 95% confidence intervals.
- Using the estimated model, predict the values of y when
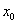 =90
and =90
and 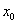 =150.
Find the 95% prediction intervals for =150.
Find the 95% prediction intervals for 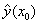 . .
|
 For
students in engineering fields. For
students in engineering fields. |
|
 For
students in toxicology and health science fields. For
students in toxicology and health science fields. |
An experiment is run to measure the cholesterol levels on 12 cardiac
patients before and after a four-month program of cardiac rehabilitation.
For each patient, a reading was taken soon after diagnosis (x) and another
was taken after a four-month program of cardiac rehabilitation (y).
Three patient were choosen at each of four levels of x. The cholesterol
levels obtained were as follows.
pretreatment_level (x) posttreatment_level (y)
180 153
180 146
180 175
200 189
200 198
200 195
220 209
220 206
220 216
240 182
240 200
240 219
- Plot the sample data in a scatter diagram. By eye, add in the line
you think fits the data best.
- Estimate the parameters in the model
 and then draw the fitted line onto your scatterplot.
and then draw the fitted line onto your scatterplot.
- Calculate the Analysis of Variance table and test the null hypotheses
of no significant regression. Use
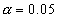
- Location the value of the t statistics for testing
 .
Use .
Use 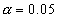 .
Show that .
Show that 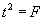 . .
- Calculate the sum of squares due to pure experimental error and
lack of fit and write the Anova table. Conduct a test for lack of
fit of the linear regression model. Does the linear regression model
fit the data well?
- Calculate the variance of
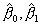 ,
compute the 95% confidence intervals for ,
compute the 95% confidence intervals for 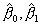 . .
- Use the estimated model, predict the values of y when
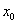 =210
and =210
and 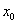 =260.
Find the 95% confidence intervals for =260.
Find the 95% confidence intervals for 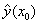 . .
|
 For
students in community development, education and social services fields. For
students in community development, education and social services fields. |
|