STA 6166 UNIT 2 Section 3 Answers
Welcome < Begin <

Section 3

 < Unit 2 Section 3 Exercises
To Ag and Env. Answers
To Tox and Health Answers
To Social and Education Answers
To Engineering Answers

Unit 2 Section 3 Answers

General Questions

What is the unbiased estimator for the population variance, s2?

The sample variance, s2. You should know the equation for this by now.

The Chi square distribution is the sampling distribution for the statistic . What can you say about the Chi Square distribution (what shape?, what parameters define its center/shape?)

The Chi Square distribution is a right skewed distribution, defined only for the positive real numbers. The shape of the distribution is defined by one parameter called the degrees of freedom. As the degrees of freedom increase, the mean of the population shifts to the right and the distribution become more spread out, i.e. the variance increases as well.

Suppose that Y has a Chi Square distribution with 27 df, using Table 7 (page 1100) find the following probabilities.
    Find P(Y>46.96)=0.01
    Find P(Y>18.11)=0.90
    Find P(Y<12.88)=1-0.99=0.01
    Find P(12.88<Y<46.96)=0.98

A random sample of sample size n=21 was collected and the sample variance computed to be 3.29. Compute the 95% confidence interval for s2. [Hint use the equation on page 346 but make sure you get the upper and lower Chi Square values correct].

n=21, (n-1)=20=df

s2 = 3.29

c2U=X2n-1,a/2 = c220,0.025 = 34.17

c2L=X2n-1,1-a/2 = c220,0.925 = 9.591

95% CI = (1.926, 6.861)

When random samples of sizes n1 and n2 have been drawn independently from two normally distributed populations, the ratio 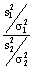has an F distribution. What can you say about the F distribution (what shape?, what parameters define its center/shape?)

The F distribution is another skewed to the right distribution. The shape of the distribution is controlled by two parameters, the denominator and numerator "degrees of freedom". How these parameters control the shape of the distribution is much more complex than with the Chi Square. As the degrees of freedom go up, the mean of the distribution shifts to the right, but only a little, while the spread of the distributions decreases. The F distribution never reaches a "normal-looking" form.

Using Table 8 (page 1102) find the value of F that has 0.05 (5%) area in the upper tail for the following degrees of freedom.
    df1=7, df2=12 F=2.91
    df1=3, df2=10 F=3.71
    df1=10, df2=20 F=2.35
    df1=8, df2=15 F=2.64

Random samples of n1=6 and n2=11 observations were selected from populations 1 and 2 respectively. The corresponding sample variances were s12=7.5 and s22=13.2. Compute the 95% confidence interval for the ratio s22/s12? [Hint use the equation on page 359 but make sure you get the degrees of freedom right.]

s22/s22 = 13.2/7.5 = 1.76

FL = 1.0/F0.025,10,5) = 1.0/6.62=0.151

FU = F0.025,5,10=4.24

95% CI = (0.151(1.76),4.24(1.76)) = (0.265, 7.462)

What would the CI look like for the ratio s12/s22?

s12/s22 = 7.5/13.2 = 0.568

FU = F0.025,10,5 = 6.62

FL =1.0/ F0.025,5,10=1.0/4.24 = 0.2358

95% CI = (0.134, 3.761)