|
STA
6166 UNIT 2 Section 3 Answers
|
| Welcome | < | Begin | < | < | Unit 2 Section 3 Exercises | |||||
| To Ag and Env. Answers |
| To Tox and Health Answers |
| To Social and Education Answers |
| To Engineering Answers |
Unit 2 Section 3 Answers
Community Development, Education and Social Services
A study was designed to evaluate whether socioeconomic factors have an effect on verbalization skills of young children. Assume two socioeconomic classes have been defined and random samples of similar-aged children from each class have been tested. Summary statistics for a verbal skills test are presented below. Perform an F-test for the difference in population variances. Given the results of this test, perform the associated two independent sample t-test for means? What do you conclude about the distributions of the two groups from these two tests?
Site n Sample_Mean Sample_Std_Dev
R1 54 3.4 3.8
R6 48 2.1 2.1
To answer this question does not require the computer but to simply implement the equations for the F-test for 2 variances followed by the appropriate t-test.
Since the Site R1 group has the largest sample standard deviation we will consider it population 1 for the F-statistic (i.e. Site R1 variance will be on the top in the ratio.) Note that we were given the sample standard deviations, hence these values will have to be squared for the test (very common mistake here).
The calculated statistic value is F=14.44/4.41 =3.274. Assume the test will be performed at the a=0.05 type I error rate (this is typical for testing variances prior to performing a two sample t-test). Thus the F statistic value will be compared to F0.025,53,47 critical value. Note that the table in our book does not have the value for df1=53 or df2=47, but the correct values should lie somewhere within these four values: F(0.025,40,40)=1.88, F(0.025,40,60)=1.74, F(0.025,60,40)=1.80 and F(0.025,60,60)=1.67. Since our observed F-statistic value is much greater than the largest of these, we would REJECT the null hypothesis of equal variances and conclude that the groups have different variances.
The previous test suggests that the two sample t-test for separate variances would be appropriate for testing the differences in the Site means. The test statistic is computed as:
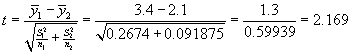
The critical value requires the calculation of the degrees of freedom using the equation on page 276 in the book.
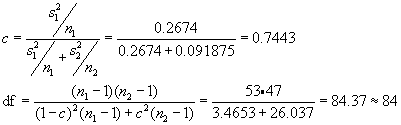
The problem description does not specify, hence we will test the two sided hypothesis at the type I error rate of a=0.05. The critical value for this test is t0.025,84 = 1.99. We reject the null hypothesis since the absolute value of the calculated t-statistic, 2.169, is greater than the critical value of 1.99. Hence we conclude that the two Sites have significantly different means as well as variances. The best estimate for the mean and standard deviation for Site R1 is 3.4 and 3.8 respectively. The best estimate for the mean and standard deviation for Site R2 is 2.1 and 2.1 respectively.
Note that a big factor in the conclusions of this study is the large sample sizes from the two groups. Even though the differences in the two means is quite small (1.3), the large sample sizes paired with the moderate sample standard deviations allow us to show that this small difference is statistically different. If would remain for you as researcher to determine if a difference of 1.3 is socially (biologically, physically) important.
Think of a situation in your studies or research where testing the equality of variances would provide useful information?