You can choose to work some or all of the problems listed below. We recommend
that you at least work the problems listed in your major area of interest.
Answers to these exercises will be posted here
(ANSWERS).
| General Questions. |
- If two independent random variables, y1 and y2,
are normally distributed with means and variances (m1,
s21) and (m2,s22)
respectively, the difference between the random variables has what
distribution (be specific - give mean and variance).
- The sampling distribution of the difference between two sample means
has an approximate normal distribution in large samples with mean
equal to what?
- The standard error of the sampling distribution of the difference
between two sample means has what value?
- The following estimate for the standard error of the difference
between two means is used when what assumption about the two population
variances can be made?
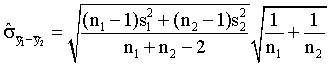
- What assumption about the two population variances is made when
the following standard error estimate is used?
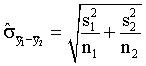
- Most of the time in two-population tests, we test the hypothesis
H0: m1-m2
=0. What does it mean to test the hypothesis H0: m1-m2
= D0 where D0 does not equal to zero?
- Why is the Wilcoxon Rank Sum test use the words "Rank Sum"
in its name?
- Use Table 5 in the Appendix to find the critical value of the Wilcoxon
rank sum test for independent samples when n1=7 and n2
= 6 and the alternative hypothesis is "Population 1 is shifted
to the right of Population 2" with Type I error probability of
a=0.05.
- How is the critical value for the Wilcoxon rank sum test found if
one or both of the sample sizes are greater than 10?
- What do we mean when we talk about "Paired Data"?
- Is a two-sample Paired Data t-test equivalent to a one-sample t-test
performed on the differences in values for each sample unit?
- Which of the two test is for testing the difference in means from
samples of two independent populations? The Wilcoxon Rank Sum Test
or the Wilcoxon Signed Rank Test? So what does the other test?
- The equation for estimating sample sizes for the two-sided hypothesis
test of differences of means is given by:
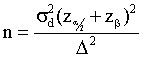 .
Can you define each of the terms in this equation? .
Can you define each of the terms in this equation?
- Do problem 6.83 as a paired samples t-test and using the Wilcoxon
Signed Rank test, both with a Type I error probability of 0.05. Do
you get different results?
- Again, using the scenario of problem 6.83 (page 334), how many water
samples would we need if we wanted to be certain that the two Analysts
did not differ by more than 2 ppm with Type I error probability of
0.05 and Power of 0.90 assuming the underlying variance in the differences
were 1.0?
Review the Key Formulas on pages 317-318.
|
 For
students in agriculture and environmental fields. For
students in agriculture and environmental fields. |
- Do problem 6.75 on page 332.
- Using the data from problem 6.75, perform the Wilcoxon rank sum
test. Do the t-test and Wilcoxon test give different results?
- What is the 95% confidence interval for the difference between the
two means?
- How many dairy cows would be needed for each group if we wanted
to know the average difference between the two groups to within plus
or minus .5 kg with 95% confidence (Hint see page 314). Use the pooled
variance estimate from the t-test as if it were the true variance.
|
 For
students in engineering fields. For
students in engineering fields. |
- Do problem 6.37 on page 319.
- Using the data from problem 6.37, perform the Wilcoxon rank sum
test. Do the t-test and Wilcoxon test give different results?
- What is the 95% confidence interval for the difference between the
two means?
- How many beams would be needed for each group if we wanted to estimate
the difference between the average loading of the two groups to be
within plus or minus 0.5 tons with 95% confidence (Hint see page 314).Use
the pooled variance estimate from the t-test as if it were the true
variance.
|
 For
students in toxicology and health science fields. For
students in toxicology and health science fields. |
Bailer and Oris (1993, Env Tox and Chemistry, 12, pp787-91) report
data from a study of toxic reproductive response in the aquatic organism
Ceriodaphnia dubia to the herbicide nitrofen. A measure of reproductive
stress in C. Dubia after exposure to the chemical is offspring counts
from exposed females. A decrease in mean response in the exposure group
suggests a toxic response to the chemical. Data from 20 independent
animals were recorded as total number of offspring for three broods
per animal.
Control 27 32 34 33 36 34 33 30 24 31
Nitrofen(160mg/l) 29 29 23 27 30 31 30 26 29 29
- Perform a t-test to compare the means of these two groups.
- Perform the Wilcoxon rank sum test to these data. Do the two test
provide the same results?
- What is the 95% confidence interval for the difference between the
two means?
- If we wanted to know the difference between the average offspring
count to within plus or minus 1 with 95% confidence, how many females
should we use for each group. Assume the pooled variance estimated
for the t-test is the true variance.
Note that these are count data. Counts are typically not very normally
distributed. Typically the analysis would be performed on transformed
data, either the square root of the counts or the natural logarithm
of the counts. Transformation of the response could change the results
of the two-sample t-test (try if for fun and see how much). The Wilcoxon
rank sum test results would not change. Do you know why?
|
 For
students in community development, education and social services fields. For
students in community development, education and social services fields. |
- Do problem 6.63 on page 327.
- Using the data from problem 6.63, perform the Wilcoxon rank sum
test. Do the t-test and Wilcoxon test give different results?
- What is the 95% confidence interval for the difference between the
two means?
- How many candidates of each gender would be needed if we wanted
to estimate the difference between the average expenditures of the
two groups to be within plus or minus $5 with 95% confidence (Hint
see page 314).Use the pooled variance estimate from the t-test as
if it were the true variance.
|
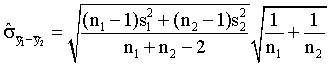
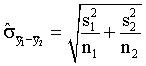
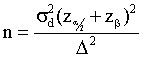 .
Can you define each of the terms in this equation?
.
Can you define each of the terms in this equation?