| > | restart; |
| > | with(plots): |
| > | assume(n,integer); |
Example 1
| > |
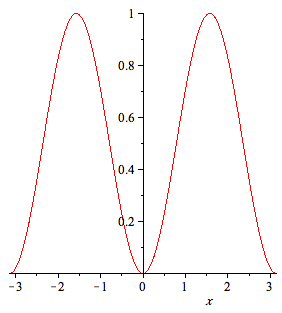
| > | f:=sin(x)^2; |
| > | a[0]:=1/(2*Pi)*int(f,x=-Pi..Pi); |
| > | a[n]:=1/Pi*int(f*cos(n*x),x=-Pi..Pi); |
Note this is not correct
| > | a[2]:=1/Pi*int(f*cos(2*x),x=-Pi..Pi); |
| > | plot(f,x=-Pi..Pi); |
 |
| > | b[n]:=1/Pi*int(f*sin(n*x),x=-Pi..Pi); |
| > |
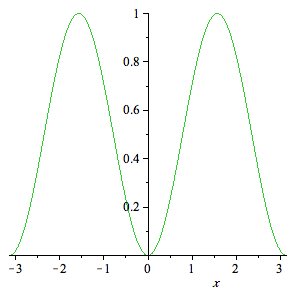
| > | fs:=a[0]+a[2]*cos(2*x); |
| > | plot({f,fs},x=-Pi..Pi); |
 |
| > |
| > |
Example 2
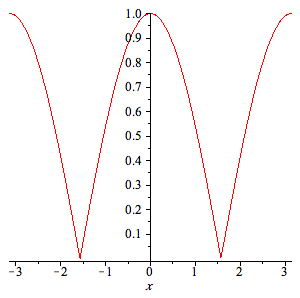
| > | f:=abs(cos(x)); |
| > |
| > |
| > | plot(f,x=-Pi..Pi); |
 |
| > |
| > | a[0]:=1/(2*Pi)*int(f,x=-Pi..Pi); |
| > | a[n]:=1/Pi*int(f*cos(n*x),x=-Pi..Pi); |
| > | a[1]:=1/Pi*int(f*cos(x),x=-Pi..Pi); |
| > |
| > | b[n]:=1/Pi*int(f*sin(n*x),x=-Pi..Pi); |
| > |
Note that when n is odd and greater than 1, a[n] = 0 and when n=1 we can use L'Hospital rule to find a[1]
| > | AA[k]:= 4*(-1)^(k+1)/Pi/(4*k^2-1); |
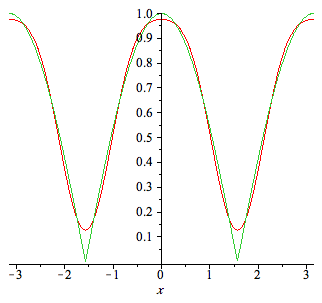
| > | fs:=a[0]+sum(AA[k]*cos(2*k*x),k=1..2); |
| > | plot({f,fs},x=-Pi..Pi); |
 |
| > | S:=(m,x)->2/Pi+sum(AA[k]*cos(2*k*x),k=1..m); |
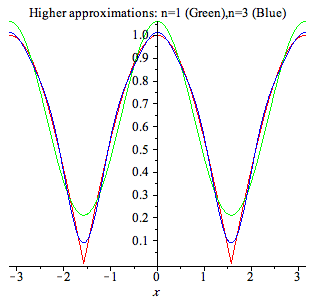
| > | plot([f,S(1,x),S(3,x)],x=-Pi-.01..Pi+0.01,title="Higher approximations: n=1 (Green),n=3 (Blue)",color=[red,green,blue],numpoints=100); |
 |
| > |
| > |
Example 3
| > |
| > | f:=Pi-x; |
| > | a[0]:=1/(2*Pi)*int(f,x=0..2*Pi); |
| > | a[n]:=1/Pi*int(f*cos(n*x),x=0..2*Pi); |
| > | plot(f,x=0..2*Pi); |
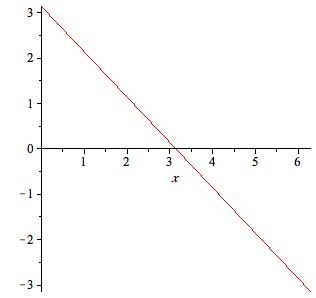 |
| > | b[n]:=1/Pi*int(f*sin(n*x),x=0..2*Pi); |
| > |
| > | B[k]:= 2/k; |
| > | S:=(m,x)->sum(B[k]*sin(k*x),k=1..m); |
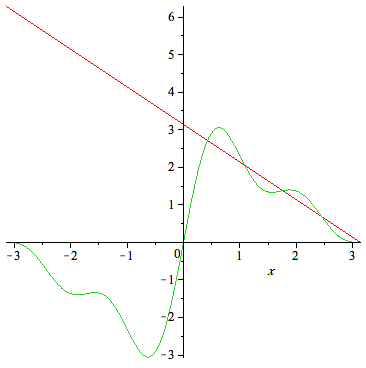
| > | plot({f,S(4,x)},x=-Pi..Pi); |
 |
| > | F:=piecewise(x<0,f-2*Pi,x>=0,f); |
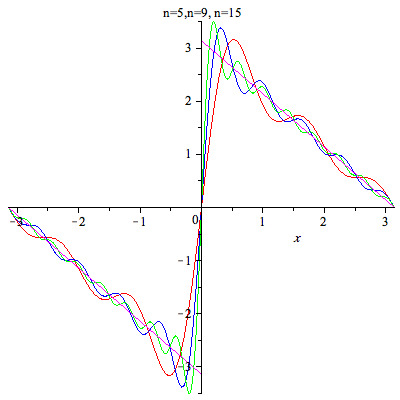
| > | plot({F,S(5,x),S(9,x),S(15,x)},x=-Pi..Pi,title=" n=5,n=9, n=15",color=[red,blue,green,magenta],numpoints=100); |
 |
| > |
Example 4
| > |
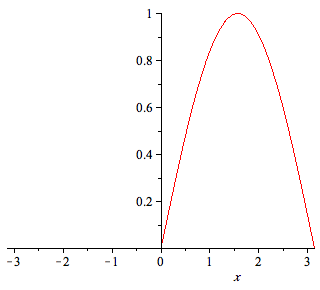
| > | f:=piecewise(x<0,0,x>=0,sin(x)); |
| > | a[0]:=1/(2*Pi)*int(f,x=-Pi..Pi); |
| > | a[n]:=1/Pi*int(f*cos(n*x),x=-Pi..Pi); |
| > | a[1]:=1/Pi*int(f*cos(x),x=-Pi..Pi); |
| > | plot(f,x=-Pi..Pi); |
 |
| > | b[n]:=1/Pi*int(f*sin(n*x),x=-Pi..Pi); |
| > | b[1]:=1/Pi*int(f*sin(x),x=-Pi..Pi); |
| > |
| > | A[k]:= -((-1)^k+1)/Pi/(k^2-1); |
| > | S:=(m,x)->a[0]+b[1]*sin(x)+sum(A[k]*cos(k*x),k=2..m); |
| > |
| > | S(8,x); |
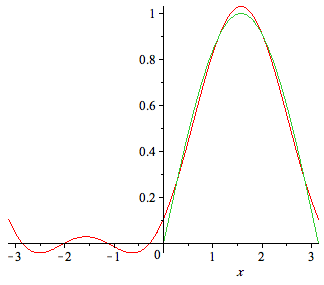
| > | plot({f,S(2,x)},x=-Pi..Pi); |
 |
| > |
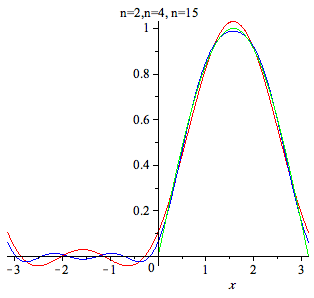
| > | plot({f,S(2,x),S(4,x)},x=-Pi..Pi,title=" n=2,n=4, n=15",color=[red,blue,green],numpoints=100); |
 |
| > |
| > |
Example 5
Consider the odd extension
| > |
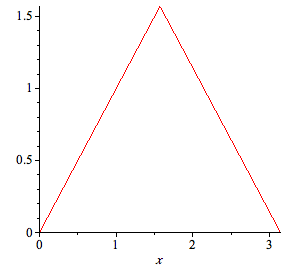
| > | f:=piecewise(x>=0 and x<Pi/2,x,x>=Pi/2 and x<Pi,(Pi-x)); |
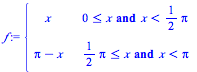 |
| > | plot(f,x=0..Pi); |
 |
| > |
| > | b[n]:=2/Pi*simplify((int(f*sin(n*x),x=0..Pi))); |
| > |
| > |
| > |
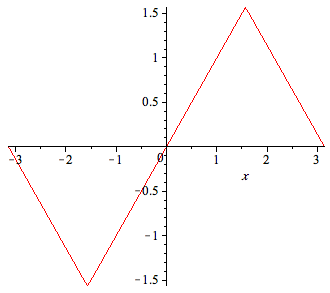
| > | ffo:= sum(b[n]*sin(n*x),n=1..100): |
| > | plot(ffo,x=-Pi..Pi); |
 |
| > |
Consider the even extension
| > |
| > | a[0]:=2/Pi*(int(f,x=0..Pi)); |
| > | a[n]:=2/Pi*simplify((int(f*cos(n*x),x=0..Pi) )); |
| > |
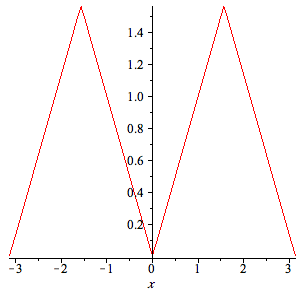
| > | ffe:= a[0]/2+ sum(a[n]*cos(n*x),n=1..100): |
| > | plot(ffe,x=-Pi..Pi); |
 |
| > |
| > |
Example 6
| > |
Consider the odd extension
| > |
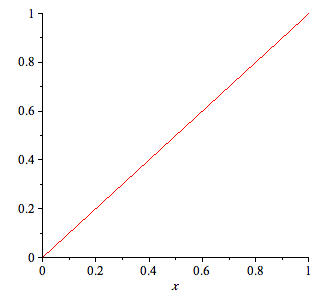
| > | f:=x; |
| > | plot(f,x=0..1); |
 |
| > |
| > | b[n]:=2*simplify((int(f*sin(n*Pi*x),x=0..1))); |
| > |
| > |
| > |
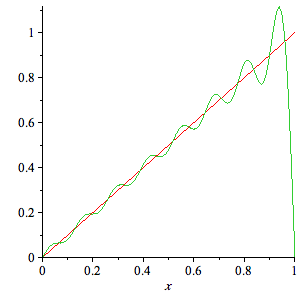
| > | ffo:= sum(b[n]*sin(n*Pi*x),n=1..15): |
| > | plot({f,ffo},x=0..1); |
 |
| > |
| > |
Consider the even extension
| > |
| > | a[0]:=2*(int(f,x=0..1)); |
| > | a[n]:=2*simplify((int(f*cos(n*Pi*x),x=0..1) )); |
| > |
| > | ffe:= a[0]/2+ sum(a[n]*cos(n*Pi*x),n=1..15): |
| > | plot({f,ffe},x=0..1); |
 |
| > |
Example 7
| > |
Consider the odd extension
| > |
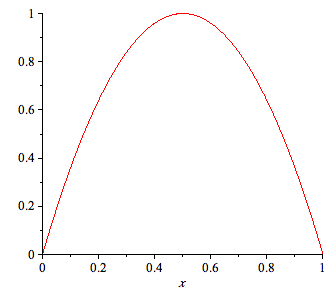
| > | f:=4*x*(1-x); |
| > |
| > |
| > | plot(f,x=0..1); |
 |
| > |
| > | b[n]:=2*simplify((int(f*sin(n*Pi*x),x=0..1))); |
| > |
| > |
| > |
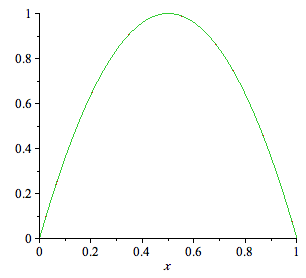
| > | ffo:= sum(b[n]*sin(n*Pi*x),n=1..15): |
| > | plot({f,ffo},x=0..1); |
 |
| > |
| > |
Consider the even extension
| > |
| > | a[0]:=2*(int(f,x=0..1)); |
| > | a[n]:=2*simplify((int(f*cos(n*Pi*x),x=0..1) )); |
| > |
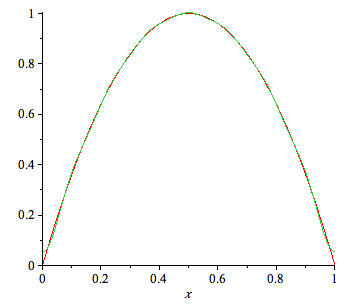
| > | ffe:= a[0]/2+ sum(a[n]*cos(n*Pi*x),n=1..15): |
| > | plot({f,ffe},x=0..1); |
 |
| > |
| > |