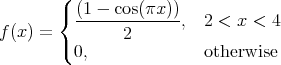
We consider an example of initial boundary value problem for the wave equation on the seni-line with Dirichlet boundary condition at x = 0:
| utt(x,t) | = uxx(x,t), 0 < x < ∞, t > 0 | (1) | |
| u(0,t) | = 0, t > 0, | ||
| u(x, 0) | = f(x), 0 < x < ∞, | ||
| ut(x,t) | = 0, 0 < x < ∞. |
Let f(x) be given by
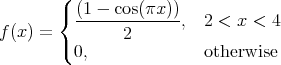
Assuming that f(x) = 0 for x < 0, we can write the odd extension  (x) of f(x) is
(x) of f(x) is
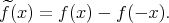
The solution 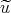 (x,t) of
(x,t) of
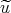 tt(x,t) tt(x,t) |
= 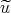 xx(x,t), -∞ < x < ∞, t > 0 xx(x,t), -∞ < x < ∞, t > 0 |
(2) | |
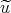 (x, 0) (x, 0) |
=  (x), -∞ < x < ∞, (x), -∞ < x < ∞, |
||
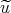 t(x,t) t(x,t) |
= 0, -∞ < x < ∞,. |
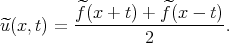
When we restrict this solution to x > 0 we obtain (recall f(x) = 0 for x < 0)
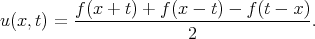 |
(3) |
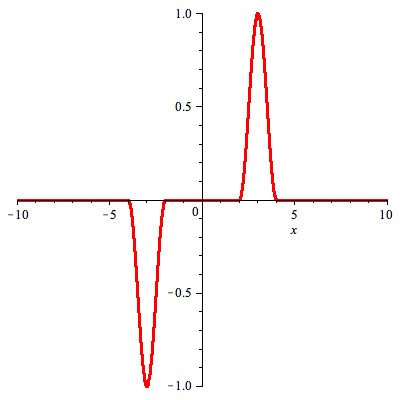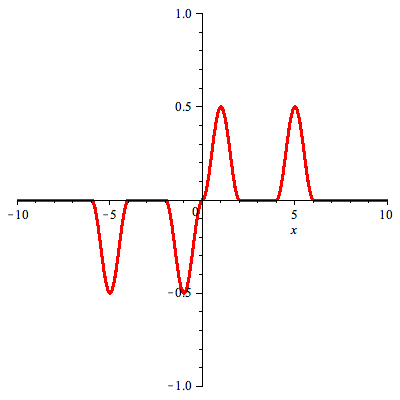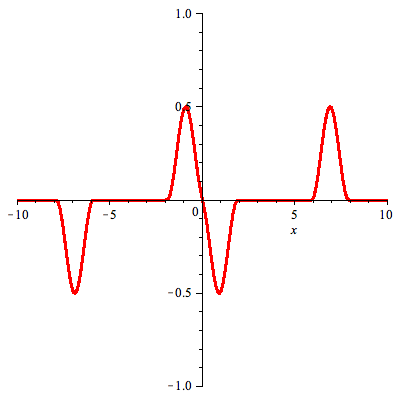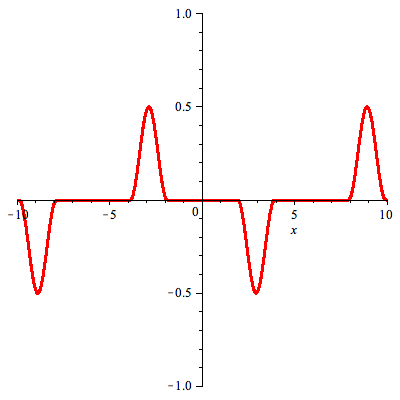
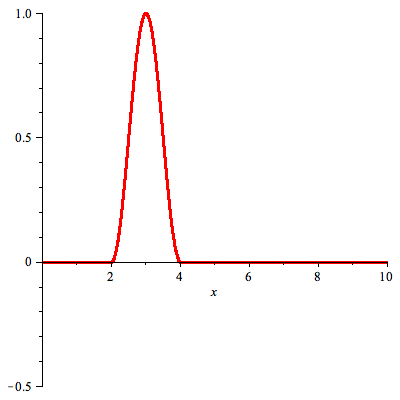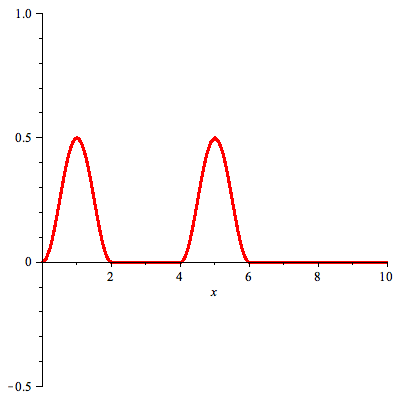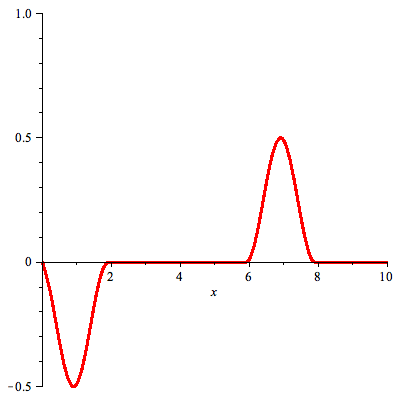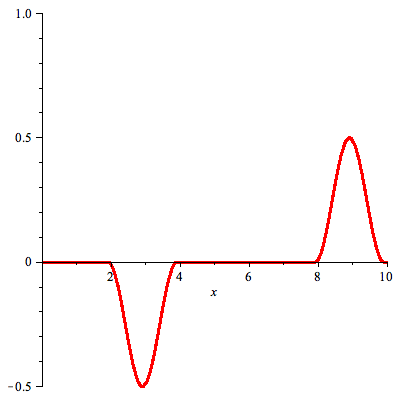
Solution of the problem on half line