STA 6166 UNIT 3 Section 2 Exercises
Welcome < Begin <

Section 2

 < Unit 3 Section 2 Exercises > Section 3

Unit 3 Section 2 Exercises

You can choose to work some or all of the problems listed below. We recommend that you at least work the problems listed in your major area of interest. Answers for these exercises can be found here. (ANSWERS)

A Note about statistical computing packages and multiple comparison procedures. Not all statistical computing packages will perform all the multiple comparisons procedures we have discussed here. Getting the computer to fit general linear contrasts is even more problematic.

 

General Questions.
  1. How is data dredging or data snooping different from performing multiple comparison procedures?
  2. The equation below provides a 95% confidence interval for the difference between two population means. What is the sp term and how is it estimated?
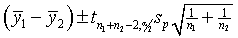
  3. Consider the following equations. Indicate with a check in the appropriate box which are true linear contrasts.

    4. Equation Contrast Not Contrast
       
       
       
       

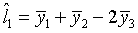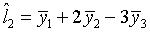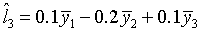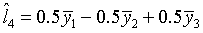  4. Is equation l1 above orthogonal to l2?
  5. In problem 8.12, page 416, Ott and Longnecker describe a strawberry preservation study involving three preservatives and a no treatment control. This resulted in four treatment groups (t=4), denoted (Control, A, B, C). Assume the four sample means are given by 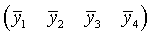respectively. For each of the following questions write a linear contrast in the four means that would be used to answer the question.
    1. Q1: Is Treatment A different from the no-treatment Control?
    2. Q2: Is the average of treatments A, B and C different from the no-treatment control?
    3. Q3: Is Treatment A different from Treatment C?
    4. Q4: Is the average of Treatments A and B different from Treatment C?
  6. In the discussion of individual comparison Type I error rates and experimentwise Type I error rates an equation is given which describes the relationship between the two. Suppose we have t=9 treatments and we wish to look at all t(t-1)=m=72 individual contrasts. What value should we use for the individual comparison Type I error rate (aI) to achieve an overall error rate of aE=0.05?
  7. Which of the following multiple comparison procedures are most conservative (in the sense that one is least likely to make a Type I experimentwise error)?
    1. Fisher's LSD
    2. Student-Newman-Keuls
    3. Tukey's W
    4. Duncan's MCP
    5. Waller-Duncan
For students in agriculture and environmental fields.
  1. Using the data and analysis from the previous exercise (Unit 3 Section 1), perform a multiple comparison analysis, with experimentwise Type I error rate of 0.05, using each of the following procedures:
    1. Fisher's LSD
    2. Student-Newman-Keuls
    3. Tukey's W
    4. Duncan's MCP
    5. Waller-Duncan

    If you transformed the data prior to the analysis of variance, the multiple comparison procedures should be performed on the transformed data as well.

  2. Using these same data, test the contrast 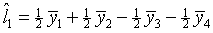where t=1 for variety A, t=2 for variety B, etc.
For students in engineering fields.
  1. Using the data and analysis from the previous exercise (Unit 3 Section 1), perform a multiple comparison analysis, with experimentwise Type I error rate of 0.05, using each of the following procedures:
    1. Fisher's LSD
    2. Student-Newman-Keuls
    3. Tukey's W
    4. Duncan's MCP
    5. Waller-Duncan

    If you transformed the data prior to the analysis of variance, the multiple comparison procedures should be performed on the transformed data as well.

  2. Using these same data, test the contrast 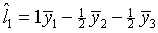where t=1 for Machine_C, t=2 for Machine_B, t=3 for Machine_A.
For students in toxicology and health science fields.
  1. Using the data and analysis from the previous exercise (Unit 3 Section 1), perform a multiple comparison analysis, with experimentwise Type I error rate of 0.05, using each of the following procedures:
    1. Fisher's LSD
    2. Student-Newman-Keuls
    3. Tukey's W
    4. Duncan's MCP
    5. Waller-Duncan

    If you transformed the data prior to the analysis of variance, the multiple comparison procedures should be performed on the transformed data as well.

  2. Using these same data, test the contrast 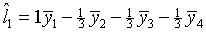where t=1 for group A, t=2 for group B, etc.
For students in community development, education and social services fields.
  1. Using the data and analysis from the previous exercise (Unit 3 Section 1), perform a multiple comparison analysis, with experimentwise Type I error rate of 0.05, using each of the following procedures:
    1. Fisher's LSD
    2. Student-Newman-Keuls
    3. Tukey's W
    4. Duncan's MCP
    5. Waller-Duncan

    If you transformed the data prior to the analysis of variance, the multiple comparison procedures should be performed on the transformed data as well.

  2. Using these same data, test the contrast 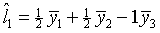where t=1 for age group A, t=2 for age group B, t=3 for age group C.