|
Section
|
Content
|
Suggested Problems
|
|
Section 3.1
|
- Initial-Value and Boundary Value Problems
- Existence and Uniqueness of IVP
- Potential Non-Existence/Non-Uniqueness of BVP
- Homogeneous Equations
- Operator Notation
- Vector Space of Solutions of Homogeneous Equation
- Linear Independence of Solutions of Homogeneous Equation
- Theorem 3.3 Wronskian Test for Linear Independence
- Fundamental Set of Solutions
- Superpostion Principle - Non-Homongenous Equations
|
|
|
Section 3.2
|
- Reduction of Order
- Standard Form
- y2 = u(x)y1(x)
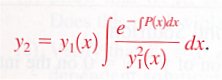
|
2, 6, 9 ,11
|
|
Section 3.3
|
- Linear, Constant Coefficient, Homogeneous
- Auxillary or Characteristic Equation
- Case I: Distinct Real Roots
- Case II: Repeated Real Roots
- Case III: Complex Conjuate Roots
- Special Cases
- y" + k2y = 0
- y" - k2y = 0
|
3, 5, 10, 13, 15, 18, 24, 31, 33, 34
|
|
Section 3.4
|
- Method of Undetermined Coefficients
- Particular Solution L(y) = f(x)
- f(x) = polynomial
- f(x) = exponential
- f(x) = cosine or sine
- Glitch in the Method
- Initial-Value Problem
|
4, 8, 12, 16, 19, 23, 28, 31
|
|
Section 3.5
|
- Variation of Parameters
- Standard Form
- Construction Fundamental Set of Solutions for Homogeneous Problem
- Solution for u1' and u2'
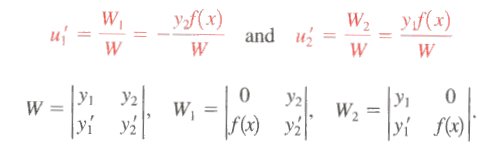
|
1, 2, 6, 8, 11
|
|
Section 3.6
|
- Cauchy-Euler Equation
- Auxillary or Characteristic Equation
- Case I: Distinct Real Roots
- Case II: Repeated Real Roots
- Case III: Complex Conjuate Roots
- Non-Homogeneous Equations
|
1, 4, 9, 11, 15, 19
|
|
Section 3.8
|
- Linear Dynamical Systems
- Hooke's Law
- Newton's Second Law
- Spring/Mass
- Equilibrium Position
- Coordinate System Orientation
- Free Undamped Motion
- mx" + kx = 0
- x" + ω2x = 0
- Alternative Form of Solution
- Free Damped Motion
- mx" + βx' + kx = 0
- x" + 2λx' + ω2x = 0
- Overdamped, Critically Damped, Underdamped
- Driven or Forced Motion
- mx" + βx' + kx = f(t)
- x" + 2λx' + ω2x = F(t)
- Transient vs Steady-State Solutions
|
3, 6, 9, 10, 21, 22, 26, 29
|

