Mesquite Trees, Anon.
Thorn Avenue
Lubbock, TX 79414

Dear Calculus Student,

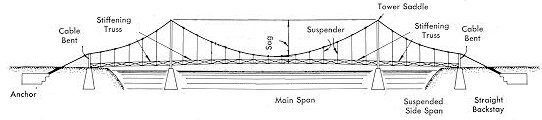
We at SlipKnot Construction Company are going to bid on a contract to build a bridge over the Brazos River chasm. At the bridge site, the chasm is 982 feet wide, so we are proposing to build a suspension bridge. There will be two towers for the suspension bridge, set in 171 feet each from the edges (so that they are 640 feet apart). Each tower will be 373 tall (from the river level to the top of the tower) and the distance from the road (bridge deck) to the top of each tower will be 250 feet.

The reason for writing you is to request some help with our computations on the length of the suspension cable. At each end the supsension cables will be attached to (land-bedded, cement) anchors which will be built 150 feet back from the chasm edge and buried 50 feet into the ground. From the anchors the cable, under tension, will run linearly to a support called the cable bent (see attached figures) which will be positioned 90 feet from the chasm edge and at a height of 10 feet. The tangential direction with which the cables will leave the cable bents to the towers will be parallel to the ground (road plane). The cables will then go up to the "saddles" at the top of the towers and, finally, hang down between the towers. Between the towers, the lower most point of the sagging cable will be 20 feet above the road (bridge deck).

We have various reference manuals which indicate that the shape of a suspended cable fits the pattern is called a catenary. According to our reference manuals, Gottfried Leibniz and Christian Huygens in 1691 determined that any cable hanging under the force of gravity must have the shape of the graph y(x) = a cosh(x/a) + b. The parameter a is the ratio of cable tension to cable density and cosh(x) = (e^x + e^-x) / 2. The only use of the parameter b is to provide a vertical shift, if necessary. It is clear that one equation will describe the shape of that part of the cable which lies between the cable bents and the towers and another equation will describe the shape of that part of the cable which lies between the two towers. We are going to assume that for each of these two parts of the cable, the shape can be described as a catenary. The part of the cable which lies between the cable bent and the anchor can be modelled by a linear equation.

From the suspension cable there will be spaced cables called "suspenders" which will drop vertically to the bridge deck. These suspenders hold the bridge deck up. Between the two towers there will be nine equally spaced (at the bridge deck) suspenders. Between the cable bents and the towers there will be two equally spaced (at the bridge deck) suspenders.

SCC would like to hire your group to find four things for us.

• First, assuming a model of a catenary for the part of the hanging cable between the two towers, what values must a and b have in order for a catenary to fit the constraints imposed by the placement of the towers and the low point of the cable between the towers? We are especially interested in the parameter a since this will tell us what tension the cable will be under.
• Second, assuming a model of a catenary for the part of the hanging cable between the towers and the cable bents, what values must a and b have in order for a catenary to fit the constraints imposed by the placement of the towers and the cable bents and the tangential direction of departure of the cable at the cable bents? Again, we are especially interested in the parameter a since this will tell us what tension the cable will be under.
• Third, what total length cable will we need? There will be, of course, a suspension cable for each side of the bridge. It will be sufficient to calculate the length cable for just one side of the bridge.
• Fourth, what will be lengths of the each of the suspenders? Again, there will be suspenders for each side of the bridge. It will be sufficient to calculate the lengths of the suspenders for just one side of the bridge.

We look forward to receiving your analysis of this problem. The final 3--5 page report should be submitted by the 23th of April. As is our policy, we have arranged that a qualified (if erratic) mathematician in the area, the estimable Dr. Pearce, be available to answer any questions you may have in the course of your work.

We look forward to hearing from you.

Sincerely

Roy Bean
President, SCC

rb:hs

All reports submitted to SlipKnot Construction Company should be written so that the directors receiving the report can understand and apply the information contained therein. Owing to SlipKnot Construction Company preeminent position in the construction arena all of our project managers have degrees in civil engineering, and thus have had college level mathematics, including calculus---unfortunately, however, their long experience in the field precludes a ready knowledge of the same. Therefore, the reports should assume a strong precalculus and basic calculus (about half a semester of calculus I) background, but should not expect a knowledge of much more than that.

Reports should further:

• Be written in the first person plural (e.g., "We found the requisite data from the figure...").
• Include mathematical formulas and appropriate graphs in the body of the report as appropriate to describe the methods and results obtained. (While the report must be typewritten, it is fine to neatly hand-write formulas if that significantly simplifies its generation.)
• Clearly explain how the mathematical formulas that are included bear on the problem being solved.
• Consist of:
  • An Introduction, describing the problem to be solved, and an indication of the mathematical method used to solve it.
  • A Body, describing the mathematical problem that was solved to answer the question(s) posed in the introduction, and the solution to it.
  • A Conclusion, summarizing the results obtained from the solution described in the body and clearly stating their relevance to the original problem as described in the introduction.
  • Be 2.5--5 pages in length, excluding supporting figures and diagrams in an attached appendix.