Mesquite Trees, Anon.
Thorn Avenue
Lubbock, TX 79414
Dear Calculus Student,
You don't know me - my name is Cleever Kapoot, but you may remember my neighbor, Betty. She related to me how helpful and resourceful you were on a project she placed across your desk last semester.
I am the CEO of Medres, Inc., a world-leader in applied medical research. We have recently completed the purchase of a small hospital here in Midland, TX. As it happens, this hospital has a sports medicine and research division that is concerned with the development of athletes to their full potential, and it is on this matter that we are contacting your company.
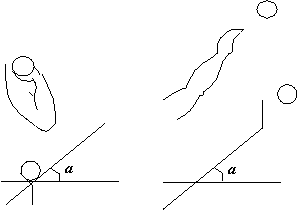
Several of the clients of this division are a shot-putters at a local college who are intent on improving their performance and are therefore interested in an analysis of aspects of their shot-putting style. Critical to the distance to which a shot may be "put" is, of course, the force that may be exerted in the extension of the putter's arm from fully contracted to fully extended (figure 1). We made a few measurements with our shot-putters (in their weight training), to try to compute the available force as a function of the angle a at which the shot is released. Our data is shown in table 1.
 |
| Figure 1: Shot put |
| a | 0o | 30o | 70o | 90o |
| F | 300 | 270 | 230 | 210 |
| Table 1: Force, in pounds, exerted by shot-putter as a function of release angle a. | ||||
We have made an assumption, given our data, which we would like you to incorporate into your analysis of our problem, that the available force to the shot-putter is a linear function of the release angle.
Given this force, the release velocity of the shot may be found from Newton's law to be approximately vR = 4.08 ((2A/m) F)1/2, where A is the extended length of the putter's arm and m the mass of the shot. (The vertical and horizontal components of this velocity are then vR sin(a) and vR cos(a).)
The answer that we need for the shot-putters group is therefore at what angle the shot should be released to maximize the distance that the shot is put. For all practical purposes, it may be taken that the shot leaves the hand of the shot-putter at a height of 6 feet and that the playing field is flat (i.e., the ground where the shot eventually hits is height 0). In your analysis, please consider several typical arm lengths -- for our shot-putters these range between 2'3" to 2'9".
We look forward to receiving your analysis of this problem. The final 3--5 page report should be submitted by the 29th of January. As is our policy, we have arranged that a qualified (if erratic) mathematician in the area, the estimable Dr. Pearce, be available to answer any questions you may have in the course of your work.
We look forward to hearing from you.
Sincerely
Cleever Kapoot, MD
President, Medres, Inc.
ck:hs
All reports submitted to Medres, Inc. should be written so that the directors receiving the report can understand and apply the information contained therein. Owing to the preeminent position of Medres, Inc.in the field, all of our directors have degrees in science, and thus have had college level mathematics, including calculus---unfortunately, however, their long experience in the field precludes a ready knowledge of the same. Therefore, the reports should assume a strong precalculus and basic calculus (about half a semester of calculus I) background, but should not expect a knowledge of much more than that.
Reports should further: