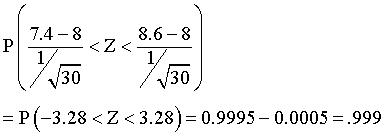You can choose to work some or all of the problems listed below. We recommend
that you at least work the general questions and the problems listed in your
major area of interest. When you finish, check yourself against the answers.
Answers can be found here.
| General Questions. |
- Identify the following random variables as being either discrete
or continuous.
- Concentration of an environmental toxin in eggshells of a given
bird species.[Continuous]
- Number of mutations in a bacterial culture after exposure to
a mutagen.[Discrete]
- Understory biomass in a quarter meter survey area.[Continuous]
- Blood pressure of a heart patient in a clinical trial.[Continuous]
- Age of the same heart patient.[Discrete]
- Time to failure in a concrete pressure test.[Continuous]
- Proportion of citrus fruit on a tree that is infected by the
Mediterranean Fruit fly larvae.[Continuous]
- Number of high school graduates in a sample of 100 prisoners.[Discrete]
- For each of the following pairs of events, decide whether or not
the events are independent. Can you explain why?
- The number of eggs laid (A) and the concentration of toxins
in the eggshell (B) for birds living in a contaminated ecosystem.[Not
independent - Higher concentrations in the eggshell would be indicator
of hight concentrations in the mother. Higher contaminated mother
less likely to have large numbers of eggs.]
- Failure of a metal beam (A) and the size of the load imposed
on it (B).[Not independent - the higher
the load the more likely the beam is to fail, assuming all beams
are of the same size.]
- The height (A) and weight (B) of an individual. [Would
be expected to not be independent since the taller the individual
the more weight they are expected to have. Note that the relationship
does not have to be exact for independence to be rejected.]
- The age (A) and gender (B) of an individual. [Would
be expected to be independent except at the extreme old age -
where females tend to live longer. At most other ages, there is
a 50:50 split in the population.]
- The number of telephone poles in a county (A) and the number
of lung cancer deaths per year (B). [We
would expect these to be independent since one would have to work
very hard to come up with a hypothesis to explain a relationship
between the two. Nevertheless, there is a significant correlation
between these two variables, hence statistically they are not
independent.]
- Work problem 4.28 in Ott and Longnecker, page 140. Can you rewrite
this problem for a common situation in your area of study?
- Which of the following are valid probability (mass) density functions?
-
| x |
0
|
2
|
4
|
6
|
8
|
| P(X=x) |
0.2
|
0.2
|
0.2
|
0.2
|
0.2
|
Yes this is a pdf.
-
| x |
-2
|
-1
|
0
|
1
|
| P(X=x) |
0.22
|
0.31
|
0.23
|
0.24
|
Yes this is a pdf.
-
| X |
0
|
1
|
2
|
3
|
4
|
5
|
6+
|
| P(X=x) |
0.06
|
0.21
|
0.33
|
0.31
|
0.21
|
-0.19
|
0.08
|
No way! You can never have a probability
less than zero.
- Let Y be a binomial random variable. Compute the following probabilities.
[ All can be solved with the equation from page 146. Note that for
part c here, you have to add up the probabilities from zero to 12
(13 not included).]
- Let n=10, p=0.2, compute P(Y=3).[0.201]
- Let n=4, p=0.4, compute P(Y=2).[0.346]
- Let n=16, p=0.7, compute P(Y<13).[0.754]
- Use Table 1 in the Appendix of Ott and Longnecker to find the area
under the standard normal curve for the following.
- For z between 0.0 and z=1.3 [0.9032-0.5
= 0.4032]
- For z between -1.0 and z=1.0 [0.8413 -
0.1587 = 0.6826]
- For z between 0.0 and z= -1.3 [.5000 -
0.0968 = 0.4032]
- For z greater than 1.75 [1.0 - .9599 =
0.0401 ]
- For z less than -1.75 [ Same as d by symmetry
]
- Using Table 1, find the value of z, call it z0, such
that P(Z>z0) = 0.25. [ .677 ]
- Suppose that Y is a normal random variable with m
= 100 and s = 15. Compute the following
using Table 1 in the Appendix.
- P(Y<100) [ = P(z<(100-m)/s)=P(z<0)
= 0.5000 ]
- P(Y>110) [ = P(z>(110-100)/15) =
P(z>0.67) = 1.0-0.7486=0.2514 ]
- P(88 < Y < 120) [ = P((88-100)/15
<z < (120-100)/15) = P( -0.8<z<1.33) = P(z < 1.33)-P(z<-.8)
= 0.9082-0.2119 = 0.6963 ]
- P(100 < Y < 108) [=P(z<(108-100)/15)-P(z<(100-100)/15)
= P(z<0.53)-P(z<0) = 0.7019-0.5000 = 0.2019 ]
- Find the value k such that P(100 - k < Y < 100 + k) =
0.6 [ k=12.6 check it out for yourself.
]
- State in your own words what the Central Limit Theorem for the Sample
Mean says. [I would never put words in your
mouth.]
|
 For
students in agriculture and environmental fields. For
students in agriculture and environmental fields. |
- As part of a wading bird research project in the Florida Everglades,
you monitor nesting in two large egret rookeries for egg laying and
nesting success. Results are described in the table below.
| |
Number of Nests Examined
|
Number of Nests with Eggs
|
Number of Nests with Hatchlings
|
| Rookery 1 |
103
|
37
|
17
|
| Rookery 2 |
92
|
21
|
9
|
| Total |
195
|
58
|
26
|
Using this table compute the following:
- What is the (estimate of the) probability of finding an egg
in a nest? [58/195 = 0.297 ]
- What is the conditional probability of finding an egg in a nest
given it is from Rookery 1? [37/103 = 0.359
]
- What is the probability of a nest producing a hatchling? [
26/195 = 0.133 ]
- What is the conditional probability of a nest producing a hatchling
given that the nest has been reported as having at least one egg?
[ 26/58 = 0.448 ]
- Are the estimates of the conditional probability of a nest producing
a hatchling the same for Rookery 1 as for Rookery 2.
[ Rookery 2 conditional probability is 21/92 = 0.228 which is
less than the 0.359 of Rookery 1. It would be nice to have a statistical
test here to determine the probability that these numbers are
really different.]
- Yield of a particular fruit is known to be normally distributed
with mean of 10 kg/tree and standard deviation of 2 kg/tree. Suppose
yields of twenty trees are to be collected and the average computed.
What is the probability of observing an average yield below 9 kg/tree?
(HINT: use the Central Limit Theorem to tell you what the sampling
distribution of the mean should be, compute the z-score for 9 kg/tree,
then find the appropriate probability using Table 1).
The problem can be formulated as follows: Let
Y be the random variable representing average tree yield. We
want to compute P(Y < 9). Now, if Y is an average from a population
with mean 10 and standard deviation 2, the Central Limit Theorem says
that the new standardized random variable Z = (Y-10)/(2/sqrt(n)) has
a standard normal distribution. The n here is 20. Hence we want to
know P(Z < (9-10)/(2/sgrt(20))) or P(Z < -2.23) = 0.0129.
|
 For
students in engineering fields. For
students in engineering fields. |
- The emergency room of a hospital has two large backup generators,
either of which can supply sufficient electricity for basic operations
in the event of loss of power from the regional grid. Each generator
is tested a number of times over a year with the results given below;
|
Number of times tested
|
Number of times it failed to start
|
| Generator 1 |
104
|
3
|
| Generator 2 |
104
|
6
|
| Total |
208
|
9
|
With this information compute the following:
- What is the (estimate of the ) probability that Generator 1 will
fail to start? [ 3/104 = 0.029 ]
- What is the probability that Generator 1 will start?
[(104-3)/104 = 0.971 ]
- What is the probability that one or the other of the generators
will work when needed ( P(Gen 1 works or Gen 2 works)? [
This is not as simple a problem as it initially seems. First, we
need to make an assumption, mainly that the successful start of
Gen 1 is independent of the successful start of Gen 2. Now, let
A be the event that Gen 1 starts and let B be the event that Gen
2 starts. P(A or B) = P(A) + P(B) - P(A and B). P(A) = 101/104 =
.9711. P(B) = 98/104 = 0.9423. P(A and B) = P(A)P(B) =0.9151 (by
independence). Hence P(A or B) = .9711 + .9423 - .9151 = 0.9983
]
- What is the probability that both generators fail to work simultaneously
when needed ( P(Gen 1 fails and Gen 2 fails) [
If we can assume that A is independent of B, then it follows that
the complement of A should be independed of the complement of B.
Let C be the event that Gen 1 fails (complement of A) and let D
be the event that Gen 2 fails (complement of B). Then P(C and D)
= P(C)P(D) = (3/104)(6/104)=0.0017 = 1-0.9983 that is the probability
that both fail simultaneously is 1 minus the probability that at
least one of then successfully starts.]
- A robotic device for tightening a bolt is designed to produce torque
values that are normally distributed with mean of 8 ft-lbs and standard
deviation of 1 ft-lbs. We plan to tighten 30 bolts with this device,
then measure the actual torque level. What is the probability of observing
an average torque value for these 30 readings that is between
7.4 ft-lbs and 8.6 ft-lbs. (HINT: use the Central Limit Theorem to
tell you what the sampling distribution of the mean should be, compute
the z-scores for the torque limits, then find the appropriate probability
using Table 1).
Let us formulate the problem as follows. Let
T be a random variable representing the AVERAGE torque value for these
30 readings. Then T is a mean from 30 samples from a population with
expected mean of 8 and standard deviation of 1. By the Central Limit
Theorem, Z = (T-8)/(1/sqrt(30)) will have a standard normal distribution.
We want to know then
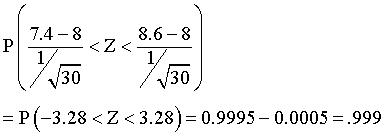
|
 For
students in toxicology and health science fields. For
students in toxicology and health science fields. |
- A simple bioassay is performed to determine the toxicity of a pesticide
on a infaunal copepod. The marker of aquatic toxicity was the capacity
of the copepod to produce young that grow to the adult stage (26-day
maturation). The table below presents information on the numbers of
survivors to adulthood for the control group (no pesticide) and the
treated group (40 microgram/l exposure).
| |
Sex of Offspring
|
| |
Female
|
Male
|
Total
|
| Control |
315
|
107
|
422
|
| Treatment |
229
|
93
|
322
|
| Total |
544
|
200
|
744
|
Compute the following:
- What is the probability of observing a male offspring (P(event
A=being male)? [200/744 = 0.269 ]
- What is the conditional probability of observing a male offspring
given the control group (P(A|B=being in the control group))? [
107/422 = 0.2535 ]
- What is the probability of a male offspring being also part
of the control treatment group (P(A and B)? [
107/744 = 0.144 ]
- The level of nitrogen oxide in the exhaust of a new model of car
when driven in city traffic is reported to have an approximately normal
distribution with mean of 1.4 g/km and standard deviation of 0.19
g/km. We plan to take exhaust readings from 22 cars and compute their
average NO exhaust level. What is the probability of observing a mean
that is below 1g/km? (HINT: use the Central Limit Theorem to tell
you what the sampling distribution of the mean should be, compute
the z-scores for 1 g/km, then find the appropriate probability using
Table 1).
If you looked at the problems above you get
the idea how to answer this question. Let X be the random variable
representing the average NO exhaust level from 22 sample cars from
a population with mean 1.4 and standard deviation 0.19. Then from
the Central Limit Theorem, we are interested in P(X < 1) = P (
Z=(X-1.4)/(0.19/sqrt(22))<(1-1.4)/(0.19/sqrt(22)) = P(Z < -9.87
) = 0.00000. That is, it is almost impossible that the NO exhaust
average of the 22 sample cars will be less than 1 g/km (assuming that
they come from the stated population.) ]
|
 For
students in community development, education and social services fields. For
students in community development, education and social services fields. |
- (From Ott and Longnecker, p135, #4.16) A survey of a number of large
corporations gave the following probability table for events related
to the offering of a promotion that also involved a location transfer.
|
|
Married
|
|
|
|
Promotion/Transfer
|
Two-Career Marriage
|
One-Career Marriage
|
Unmarried
|
Total
|
|
Rejected
|
.184
|
.0555
|
.0170
|
.2565
|
|
Accepted
|
.276
|
.3145
|
.1530
|
.7435
|
|
Total
|
.46
|
.37
|
.17
|
|
Using this table compute the following:
- What is the probability that a professional (selected at random)
would accept the promotion? [ .7435 ]
- What is the probability that a professional (selected at random)
is part of a two-career marriage? [0.46]
- What is the conditional probability of accepting the promotion,
given the professional is part of a two-career marriage?
[P(A|B) = P(A and B)/P(B) Let A be the event
of accepting the promotion and B be the event that the individual
is part of a two-career marriage. P(B) = 0.46. P(A and B) = 0.276,
P(A|B)=0.276/0.46 = 0.6. ]
- Based on the 1990 census, the numbers of hours per day that adults
spend watching television is approximately normally distributed with
a mean of 5 hours and a standard deviation of 1.3 hours. We plan to
survey 50 adults and record the number of hours they watch television
in a day. What is the probability that the average number of hours
for our sample exceeds 6 hours per day? (HINT: use the Central Limit
Theorem to tell you what the sampling distribution of the mean should
be, compute the z-scores for 6 hours per day, then find the appropriate
probability using Table 1).
Let H be the random variable representing the
average number of hours for 50 individuals sampled from a population
with mean 5 and standard deviation 1.3. We want to know P(H > 6).
From the Central Limit Theorem we know that the distribution of a
standardized mean, Z= (H-5)/(1.3/sqrt(50)), will be a standard normal
distribution. Thus P(H>6) = P(Z>(6-5)/(1.3/sqrt(50))) = P(Z>5.44)
< 0.0001. Hence it is almost impossible for us to observe a average
of 6 hours in a sample of 50 individuals who come from this population.
If we did observe a mean of 6 this would strongly imply that the true
population mean was not 5.
|