Unit 1 Section 2 Exercise Answers

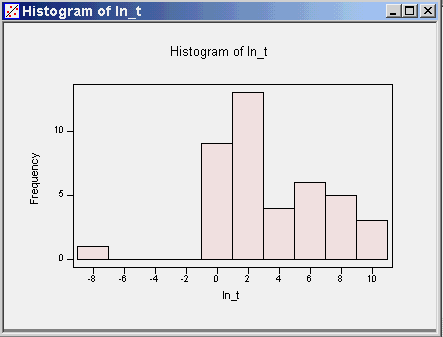
Using the data from Problem 3.65, page 112 in Ott and Longnecker, compute the following statistics. The transmissivity values are transformed by first taking their natural (base e - ln) logarithms (you will need a calculator or computer for this). We will refer to this new (derived response) as the ln transmissivity.

1. The mean of ln transmissivity for the pilot facility.
2. The median of ln transmissivity for the pilot facility.
3. The mode of ln transmissivity for the pilot facility.
4. The standard deviation of ln transmissivity for the pilot facility.
5. The coefficient of variation of ln transmissivity for the pilot facility.
6. The proportion of observations with ln transmissivity greater than 3.0.

Output from Minitab
Descriptive Statistics: ln_t

Variable             N       Mean     Median     TrMean      StDev    SE Mean
ln_t                   41      3.402      2.312       3.457        3.537      0.552

Variable       Minimum    Maximum         Q1         Q3
ln_t              -7.191      9.642                1.010     6.373

Mode is undefined since every number is different from every other number. No one number is most often found.

Coefficient of Variation = Standard deviation/mean = 3.537/3.402 = 1.039.

Proportion with Ln(Trans)> 3.0 = 18/41 = 0.439 

With these statistics answer the following.

1. Without looking at a plot of these data, would you think the histogram of ln transmissivity would show skewness? (HINT: what do we know about the relationship among the mean, median and mode for skewed data?)

Note that the median is about in the middle of the max and min, but the median is closer to Q1 (lower quartile) than to Q3 (the upper quartile) suggesting that the bulk of the data lie on the low side. The mean is larger than the median, suggesting there may be some large values in the upper tail. These tell me that the data may be a little skewed to the right.

2. Create a histogram for these data. How many bars would you use?

There are 41 observations and the range of the data is roughly 17. I let minitab choose the number of bins and it used 10.



3. Are there apparent outliers in these data.

Looks like there are some extremely low numbers that do not seem to fit in with the rest of the data.

Using the data from Problem 3.55, page 108 in Ott and Longnecker, compute the following statistics.

1. The mean Deviations from Target for each Supplier.
2. The standard deviation of the Deviations from Target for each Supplier.
3. The coefficient of variation of the Deviations from Target for each Supplier.
4. The proportion of observations greater than 190 in each group.

Results for: ex3-55.mtw

Descriptive Statistics: deviations by supplier


Variable   supplier          N       Mean     Median     TrMean      StDev
deviation     1                 9     189.23     189.90     189.23       2.96
                  2                 9     156.28     156.90     156.28       3.30
                  3                 9     203.94     204.40     203.94       8.96

Variable   supplier    SE Mean  Minimum    Maximum         Q1         Q3
deviation     1              0.99     183.80       192.80         186.95     191.40
                  2              1.10     150.90       161.50         153.20     158.25
                  3              2.99     187.10       218.60         198.55     209.75

With these statistics, answer the following.

1. Is there a supplier that provides a product that is close to the target while also being less variable.

We want the supplier to have small average deviations from target power as well as small variability. Supplier 2 produces the product with the smallest average deviations, but Supplier 1 produces the product that has smallest standard deviation. Hence there is no one supplier that satisfies both conditions.

2. What plot would you use to demonstrate the differences in Deviations from Target among the Suppliers.

A set of box-plots allows us to see very dramatically how the three suppliers differ. This tells me that although Supplier 2 does not have the smallest variance its IQR is not much different from Supplier 1. Maybe with a little better Quality Control this Supplier could provide an excellent product.

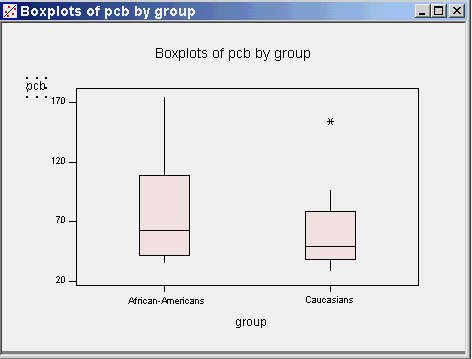
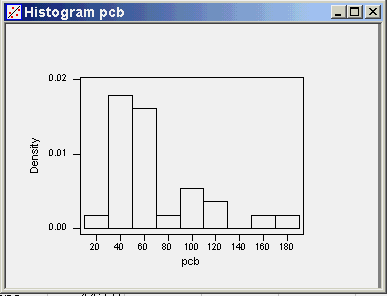
In a study of the accumulation of polychlorinated biphenyls (PCBs) in humans after chronic environmental exposure, Patterson, et. el. (1994, Env. Health Persp., 102, Supp 1, p195-204) reported the following observations for parts per trillion of PCB (lipid adjusted) in adipose tissue from the following two groups (gender unspecified).

Caucasians: 56.7,44.5,48.2,96.5,91.0,34.2,154.0,34.5,41.8,66.4,29.5.49.0,54.7

African-Americans: 36.7, 174.0, 118.0, 69.9, 62.2, 112.0, 42.0, 67.7, 59.5, 36.4, 62.4, 109.0, 84.0, 35.6, 61.6

Using these data compute the following statistics.

1. The concentration mean for each group.
2. The concentration standard deviation for each group.
3. The concentration coefficient of variation for each group.
4. The proportion of observations less than 50 ppb for each group.

Descriptive Statistics: pcb by group

Variable   group             N       Mean      Median     TrMean      StDev
pcb        African-         15      75.40       62.40      70.88      38.43
            Caucasia        13      61.62       49.00      56.14      34.46

Variable   group       SE Mean    Minimum    Maximum         Q1         Q3
pcb        African-       9.92      35.60     174.00      42.00     109.00
           Caucasia       9.56      29.50     154.00      38.15      78.70

With these statistics, answer the following.

1. Construct side-by-side box plots of these data. Does it appear that the variation in the two groups are similar?

The two groups do not appear to be very similar. Medians and Q3 values are different, while Q1 and min values are similar. African-Americans seem to have a longer right tail whereas there seems to be an outlier in the Caucasian dataset. How much of this is the low sample size one cannot tell.

2. Combine the data from the two groups and construct a histogram. Do these data appear to have a symmetric unimodal distribution?

These data do not appear to have a symmetric unimodal distribution. In fact, it appears to have three "humps" suggesting maybe there are three "populations" here rather than two. Sample sizes are quite small so no firm conclusions should be drawn.

Using the data from Problem 3.53, page 108 in Ott and Longnecker, compute the following statistics.

1. The average age for each group.
2. The standard deviation of age for each group.
3. The coefficient of variation of age for each group.
4. The percentage of the individuals in each group less than 50 years old.

Well, my hats off to any of you that attempted this problem. It is not a particularly good exercise and I wish now I had not included it. The computations for the statistics requested require that you use the mean and variance equations for grouped data (see page 110 in Ott and Longnecker). In addition, you need to assume the age assigned to each age category is the average age for the group. What do you do for the <29 age group and the >50 age group? These are actually quite difficult questions. Here I have decided to use age values for the age groups at 25, 35, 45 and 55 years. You could do the same problem with other ages for the groups if you had additional knowledge about the true average age in each group. With this assumption, the statistics are:

An Excell spreadsheet showing these computations can be downloaded from here.

With these statistics answer the following.

1. Which group has the lowest average age? (does this make sense?) The transferred group has the lowest average age, but not by much. Not sure this makes a lot of sense. Note that the Resigned group has almost the same average age, but a much larger standard deviation.
2. What graph would you use to demonstrate the differences between the two groups? Construct that graph. What does it tell you?

This is a Hi-Low plot out of Excell. This shows the mean with ±2 StdDev. With grouped data it is much harder to get a good descriptive plot since the grouping hides a lot of detail. The graph shows the transferred group to be younger and less variable with the resigned group the most variable.