|
Sicherman Dice |
|
|
When we roll two ordinary dice and add the outcomes, we get the numbers between
two and twelve with different probabilities: The chance of getting seven is 1/6,
whereas the chance of getting two is only 1/36.
|
|
|
In one of his Mathematical Games columns in Scientific American
from 1978, later reprinted in Penrose Tiles to Trapdoor Ciphers,
Martin Gardner describes the following problem, originally asked and answered by
George Sicherman of Buffalo, NY:
|
|
|
Is it possible to number the sides of two dice with positive integers in some other way,
and still have the sums give the numbers 2,...,12 with the same probabilities as with
ordinary dice?
|
|
|
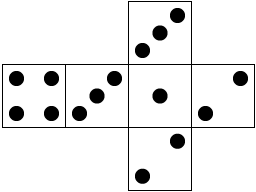
It turns out that there is in fact one other way of doing it, by numbering the sides of
one die with the numbers 1, 2, 2, 3, 3 and 4, and those of the other with 1, 3, 4, 5, 6 and 8:
|
|
|
|
Of course, this can be verified simply by making a table and checking that there is one way of
getting 2, two ways of getting 3, etc. However, there is a more algebraic approach, that will
also show that this is in fact the only alternative numbering:
|
|
|
To a die we associate a generating polynomial
by taking a term xd for each side of the die with value d.
Thus, for an ordinary die
|
|
|
|
the generating polynomial is
x6+x5+x4+
x3+x2+x,
whereas the generating polynomials for the two Sicherman dice above are
x4+2x3+2x2+x and
x8+x6+x5+x4+
x3+x,
respectively.
|
|
|
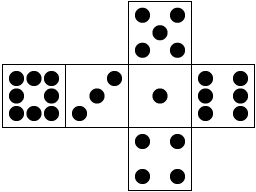
Other examples: In some stores, it is possible to buy a pair of false dice, marked like this:
|
|
|
|
Since normally only three sides of a die are visible at a time, they will look like ordinary dice,
while increasing your chances of rolling 7 from 1/6 to 1/3. Their generating polynomials are,
respectively, 2x6+2x5+2x4 and
2x3+2x2+2x.
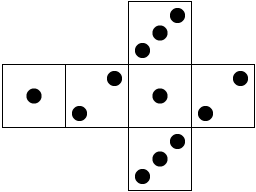
Similarly, the generating polynomial for the false die
|
|
|
|
is 2x6+x5+x4+x3+
x2.
|
|
|
All this works for any kind of die (with non-negative numbering), regardless of the number
of sides. Gaming dice with four, ten, twelve, etc., sides have generating polynomials as well.
|
|
In order for a polynomial f(x) to be the generating polynomial for
some die, it is necessary and sufficient that all the coefficients in
f(x) are non-negative
integers. In that case, the number of sides on the die equals f(1).
|
|
|
Now, if we take two dice, with generating polynomials f(x) and
g(x),
and roll them together, adding up the outcomes, they can be considered as a single "compound" die,
and this die will have generating polynomial f(x)g(x):
If die #1 rolls a and die #2 rolls b, this corresponds to a degree-a term
in f(x) and a degree-b term in g(x),
which in turn produces a degree-(a+b) term in f(x)g(x).
|
|
|
For example, the generating polynomial for rolling two ordinary dice is
|
|
(x6+x5+x4+
x3+x2+x)2 =
x12+2x11+3x10+
4x9+5x8+6x7+
5x6+4x5+3x4+
2x3+x2.
|
|
|
We can now reformulate Sicherman's question as follows: Is it possible to write the above
polynomial as a product f(x)g(x) of two polynomials
f(x) and g(x) with non-negative integer coefficients,
no constant term, and f(1)=g(1)=6?
|
|
|
The irreducible factorisation of the polynomial is
|
|
x2(x+1)2(x2+
x+1)2(x2-x+1)2,
|
|
|
and if f(x) and g(x) are to have a value of 6 for x=1,
they must both have a factor x+1 and a factor x2+x+1.
Additionally, to avoid a constant term, they must both have a factor x.
This leaves only the two factors x2-x+1 to be distributed.
If we put one on each polynomial, we get two ordinary dice, and if we put both on the same
polynomial, we get the two Sicherman dice. This establishes both existence and uniqueness of
the alternative numbering: It can be done in exactly one way.
|
|
|
It is possible to consider more than two dice this way, but it does not give any new results:
If we want to number n dice with positive integers, such that they give the same
distribution of sums as n ordinary dice, the only possibility is to replace pairs of
ordinary dice with pairs of Sicherman dice: We now need to distribute factors on n
polynomials, and it is still necessary that each polynomial gets factors x, x+1 and
x2+x+1, leaving us with n copies of
x2-x+1 to distribute. But note the following about the polynomials
given above: If there is no factor x2-x+1, the quadratic term has
coefficient 2; if there is one factor, the quadratic term has coefficient 1; and if there are
two factors, the quadratic term has coefficient 0. It is quite easy to see by induction that
the quadratic term will have coefficient 2-d, if there are d factors
x2-x+1. Consequently, we cannot have more than two, leaving us with
only ordinary dice and Sicherman dice, no matter what n is.
|
|
References |
|
|
J. A. Gallian & D. J. Rusin, Cyclotomic polynomials and nonstandard dice,
Discrete Mathematics 27 (1979), pp. 245-259.
|
|
M. Gardner, Penrose Tiles to Trapdoor Ciphers, Spectrum,
Mathematical Association of America.
|
|
| Return to teaching page. |
|